How to solve for x?
Using the theorem: if three parallel lines intersect two transversals, then they divide the transversals proportionally
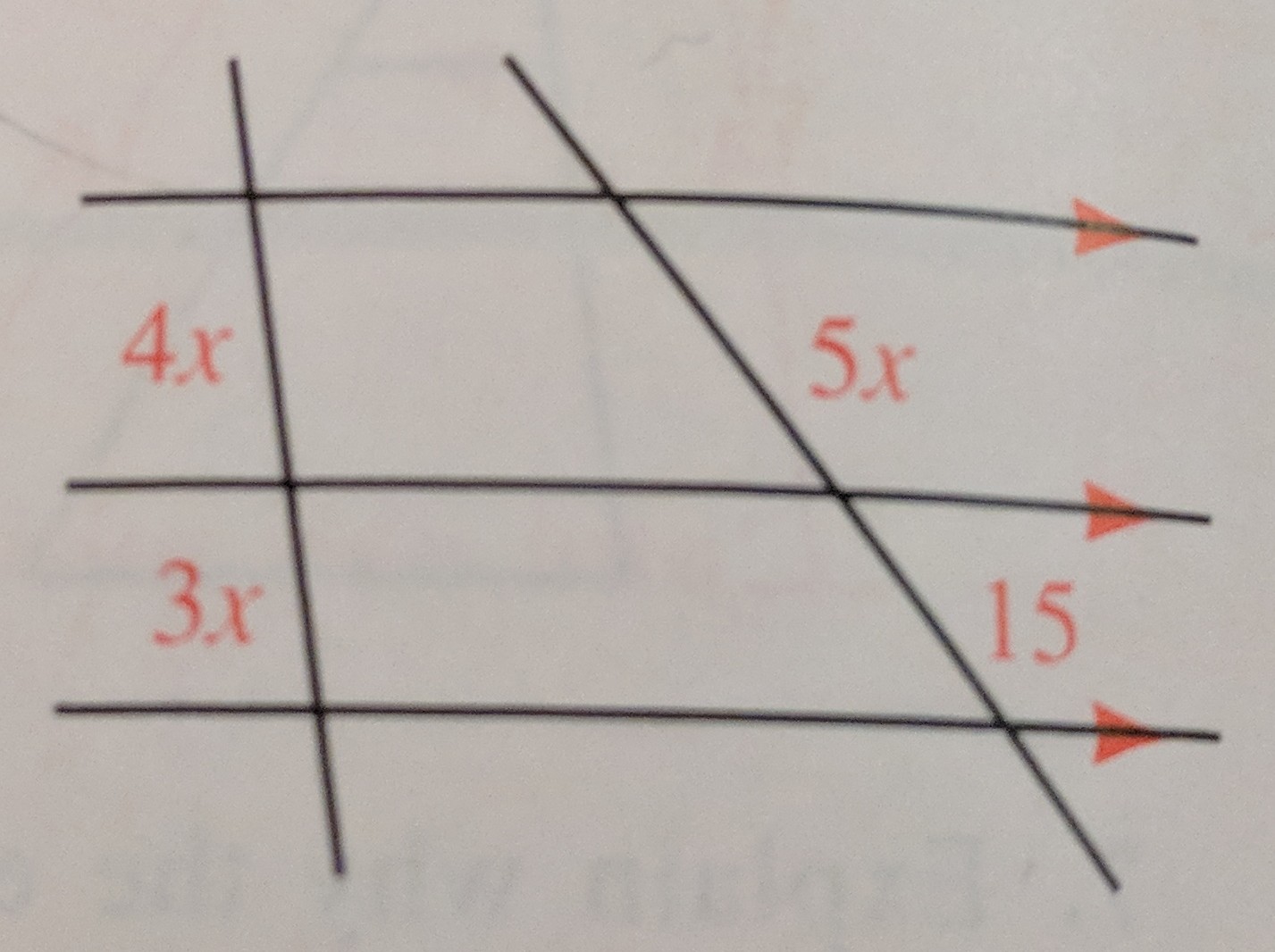
Using the theorem: if three parallel lines intersect two transversals, then they divide the transversals proportionally

1 Answer
For leftmost transversal:
For rightmost transversal:
Explanation:
The angles represented by 5x and 15 are on the same side of the transversal, so we know that the sum of those two angles will add up to 180 degrees. Consider the following equation:
x is equal to 33 degrees. For the leftmost transversal, we will have to set up another equation involving 4x and 3x. Again, they are on the same transversal, so we can set the sum equal to 180 degrees.
Plug in the x-values for the corresponding angles, and you should get 4x+3x equaling 180 and 5x+15 also equaling 180 degrees.

