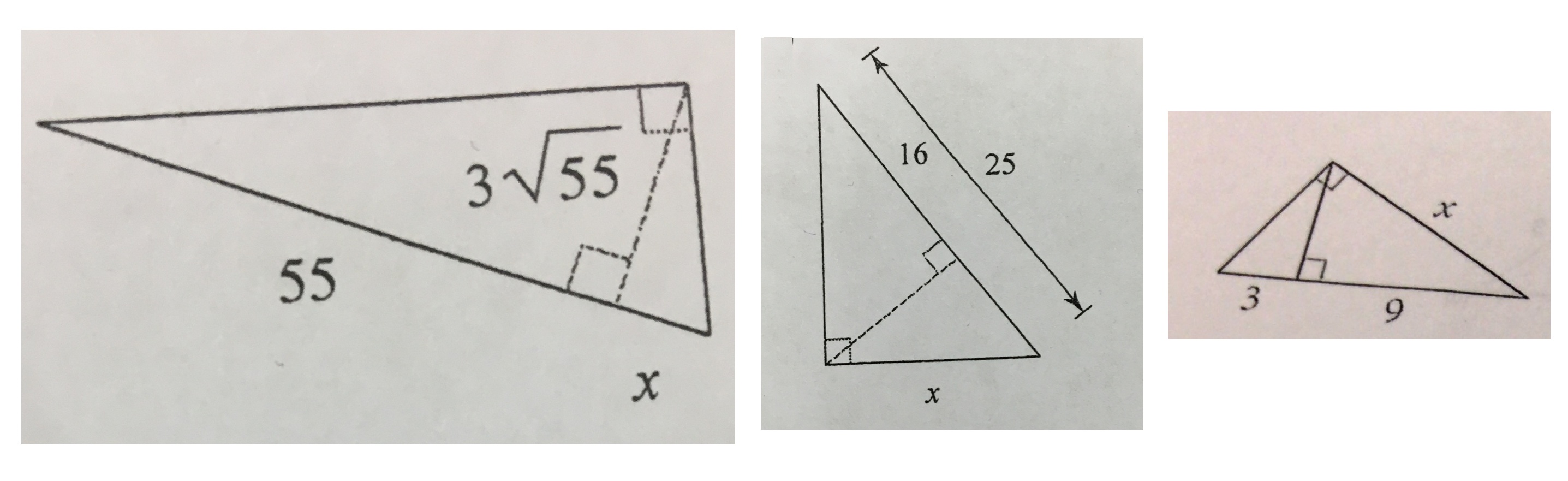
There are three diagrams:
Diagram 1:
Comparing the corresponding sides
x/(3sqrt55)=(3sqrt55)/55
55x=(3sqrt55)(3sqrt55)
55x=(9)(55)
Solving for x,
x=9
Diagram 2:
The other side in big triangle is obtained by using the pythagoras theorem as
=sqrt(25^2-x^2)
Comparing the corresponding sides
x/25=16/sqrt(25^2-x^2)
Squaring both the sides
x^2/625=256/(625-x^2)
Cross multiplying
x^2(625-x^2)=(256)(625)
Let t=x^2
t(625-t)=160000
625t-t^2=160000
t^2-625t-160000=0
Ifax^2+bx+c=0, the roots are given by
x=(-b=-sqrt(b^2-4ac))/(2a
Here,
a=1, b=-625, c=-160000, x=t
Substituting
t=(-(-625)=-sqrt((-625)^2-4(1)(-160000)))/(2(1)
=(625+-sqrt(390625+4(160000)))/2
t=(625+-sqrt(390625+640000))/2
t=(625+-sqrt(1030625))/2
sqrt1030625=1015.197
t=(625+-1015.197)/2
Let
t_1=(625+1015.197)/2=1640.197/2=820.0985=820 approximate
t_2=(625-1015.197)/2=-390.197/2=-195.0985=-195 approximate
Considering positive value,
t=820
t=^2
820=x^2
=28.637
x=sqrt820=28.637
Thus,
x=28.637
Diagram 3:
3+9=12
The other side in big triangle is obtained by using the pythagoras theorem as
=sqrt(12^2-x^2)
Comparing the corresponding sides
x/12=3/sqrt(12^2-x^2)
Squaring both the sides
x^2/144=9/(144-x^2)
Cross multiplying
x^2(144-x^2)=(9)(144)
Let t=x^2
t(144-t)=1296
144t-t^2=1296
t^2-144t-1296=0
Ifax^2+bx+c=0, the roots are given by
x=(-b=-sqrt(b^2-4ac))/(2a
Here,
a=1, b=-144, c=-1296, x=t
Substituting
t=(-(-144)=-sqrt((-144)^2-4(1)(-1296)))/(2(1)
=(144+-sqrt(20736+4(1296)))/2
t=(144+-sqrt(20736+5184))/2
t=(144+-sqrt(25920))/2
sqrt25920=160.997
t=(144+-160.997)/2
Let
t_1=(144+160.997)/2=304.197/2=152.5 approximate
t_2=(144-160.997)/2=-16.997/2=-8.498=-8.5 approximate
Considering positive value,
t=152.5
t=x^2
152.5=x^2
=12.349
x=sqrt820=12.349
Thus,
x=12.349