Question

How to solve the integral using the residue theorem `int_(-oo)^(+oo)(cos(x)/(x^4+x^2+1))dx`?

Answer 1

`int_(-oo)^(oo) ( cosx ) / ( x^4 + x^2 +1 ) \ dx = e^(-sqrt(3)/2)pi{ sqrt(3)/3cos(1/2) +sin(1/2) }`
`" " = 1.303046536141762 ...`

Explanation:

Sorry that this is such a long solution:

We seek:

`I = int_(-oo)^(oo) \ ( cosx ) / ( x^4 + x^2 +1 ) \ dx`

graph{( cosx ) / ( x^4 + x^2 +1 ) [-5, 5, -2.5, 2.5]}

The function is well defined over the domain `RR`. In order to compute this definite integral, consider the following complex variable function over a domain `CC`:

`f(z) = ( e^(iz) ) / ( z^4 + z^2 +1 ) \ \ \ \ \ (= ( cosz+isinz ) / ( z^4 + z^2 +1 ) )`

And its associated contour integral:

`oint_C \ f(z) \ dz`

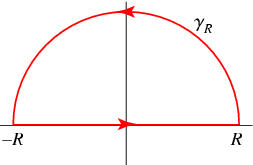
Where `C` is the following semi-circulare contour in the complex plane with radius `R gt 0`:

We will restrict `R` to enclose the poles in the upper quadrants once we have analyzed the poles of `f(z)`. The denominator of the integrand is quadratic in `z^2`, and so we can find the four simple poles of `f(z)` as follows:

`z^4+z^2+1 = 0 => =0`

`z^2-z+1 = 0 => z = \ \ \ \ 1/2+-sqrt(3)/2i`
`z^2+z+1 = 0 => z = -1/2+-sqrt(3)/2i`

We need only be concerned with the two poles in Q1 and Q2, that (providing we make `R` large enough) lie within our contour `C`

So then:

`oint_C \ f(z) \ dz = int_(-R)^(R) \ f(x) \ dx + int_(gamma_R) \ f(z) \ dz`

As `C` encloses the two poles:

`z_1 = -1/2+sqrt(3)/2i \ \` and `\ \ z_2 = 1/2+sqrt(3)/2i`

Then by the residue theorem:

`oint_C \ f(z) \ dz = 2pii xx ( ("sum of the residues of the"), ("poles of " f(z) " within "C) )`
`" " = 2pii \ { res_(z=z_1) \ f(z) + res_(z=z_2) \ f(z) }`

And we can calculate the residues as follows:

`res_(z=z_1) = lim_(z rarr z_1) (z-z_1) f(z)`
`" " = lim_(z rarr z_1) (z-z_1) ( e^(iz) ) / ( (z^2-z+1)(z^2+z+1) )`
`" " = lim_(z rarr z_1) (z-z_1) ( e^(iz) ) / ( (z^2-z+1)(z-z_1)(z-barz_1) )`
`" " = lim_(z rarr z_1) ( e^(iz) ) / ( (z^2-z+1)(z-barz_1) )`

`" " = e^(-sqrt(3)/2+1/2i) (-1/4-sqrt(3)/12i)`
`" " = e^(-sqrt(3)/2)e^(1/2i) (-1/4-sqrt(3)/12i)`

Similarly:

`res_(z=z_2) = lim_(z rarr z_2) (z-z_2) f(z)`
`" " = lim_(z rarr z_2) (z-z_2) ( e^(iz) ) / ( (z^2-z+1)(z^2+z+1) )`
`" " = lim_(z rarr z_2) (z-z_2) ( e^(iz) ) / ( (z-z_2)(z-barz_2)(z^2+z+1) )`

`" " = lim_(z rarr z_2) ( e^(iz) ) / ( (z-barz_2)(z^2+z+1) )`

`" " = e^(-sqrt(3)/2-1/2i) (1/4-sqrt(3)/12i)`
`" " = e^(-sqrt(3)/2)e^(-1/2i) (1/4-sqrt(3)/12i)`

So using these results along with the residue theorem we get:

`oint_C \ f(z) \ dz = 2e^(-sqrt(3)/2)pii{ -1/4e^(1/2i)-sqrt(3)/12e^(1/2i)i + 1/4e^(-1/2i)-sqrt(3)/12e^(-1/2i)i }`

`" " = 2e^(-sqrt(3)/2)pi{ -1/4e^(1/2i)i+sqrt(3)/12e^(1/2i) + 1/4e^(-1/2i)i+sqrt(3)/12e^(-1/2i) }`

`" " = 2e^(-sqrt(3)/2)pi{ sqrt(3)/12(e^(1/2i) + e^(-1/2i)) +1/4(e^(-1/2i)-e^(1/2i))i }`

We can simplify the expression as:

`e^(1/2i) + e^(-1/2i) = cos(1/2)+isin(1/2) + cos(-1/2)+isin(-1/2)`
`" " = cos(1/2)+isin(1/2) +cos(1/2)-isin(1/2)`
`" " = 2cos(1/2)`

And:

`e^(-1/2i)-e^(1/2i) = cos(-1/2)+isin(-1/2) -cos(1/2)-isin(1/2)`
`" " = cos(1/2)-isin(1/2) -cos(1/2)-isin(1/2)`
`" " = e^(-1/2i)-e^(1/2i) = -2isin(1/2)`

Hence:

`oint_C \ f(z) \ dz =2e^(-sqrt(3)/2)pi{ sqrt(3)/12(2cos(1/2)) +1/4(2sin(1/2)) }`
`" " = e^(-sqrt(3)/2)pi{ sqrt(3)/3cos(1/2) +sin(1/2) }`

Earlier we established that:

`oint_C \ f(z) \ dz = int_(-R)^(R) \ f(x) \ dx + int_(gamma_R) \ f(z) \ dz`

Now, as we let `R rarr oo` we get:

`oint_C \ f(z) \ dz = int_(-oo)^(oo) \ f(x) \ dx + int_(gamma_R) \ f(z) \ dz`

As is often the case with contour integrals, we find that:

`lim_(R rarr oo) int_(gamma_R) \ f(z) \ dz = 0`

I will omit the proof (as it is several pages long) but this can be verified using the Estimation Lemma.

Hence, in summary we have:

`int_(-oo)^(oo) ( e^(iz) ) / ( z^4 + z^2 +1 ) \ dz = int_(-oo)^(oo) ( cosx +isinx) / ( x^4 + x^2 +1 ) \ dx`

`" " = int_(-oo)^(oo) ( cosx) / ( x^4 + x^2 +1 ) \ dx + i \ int_(-oo)^(oo) ( sinx) / ( x^4 + x^2 +1 ) \ dx`

`" " = e^(-sqrt(3)/2)pi{ sqrt(3)/3cos(1/2) +sin(1/2) }`

Equating Real parts we then get the desired result:

`int_(-oo)^(oo) ( cosx ) / ( x^4 + x^2 +1 ) \ dx = e^(-sqrt(3)/2)pi{ sqrt(3)/3cos(1/2) +sin(1/2) }`
`" " = 1.303046536141762 ...`

As a bonus, by equating imaginary parts, we also get

`int_(-oo)^(oo) ( sinx ) / ( x^4 + x^2 +1 ) \ dx = 0`

But that should come as no surprise as the integrand is an odd function!