How to solve the simultaneous equations ∣z + 1∣ = ∣z − 1∣, ∣z + 2∣ = ∣z − 3∣?
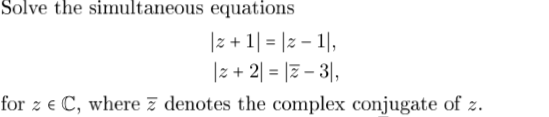
1 Answer
Apr 16, 2018
No solution
Explanation:
and
or
or
or
so no solution is possible.
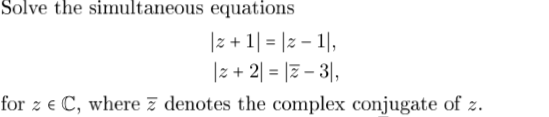
No solution
and
or
or
or
so no solution is possible.