Question

How to solve the unknown variable using calculus?

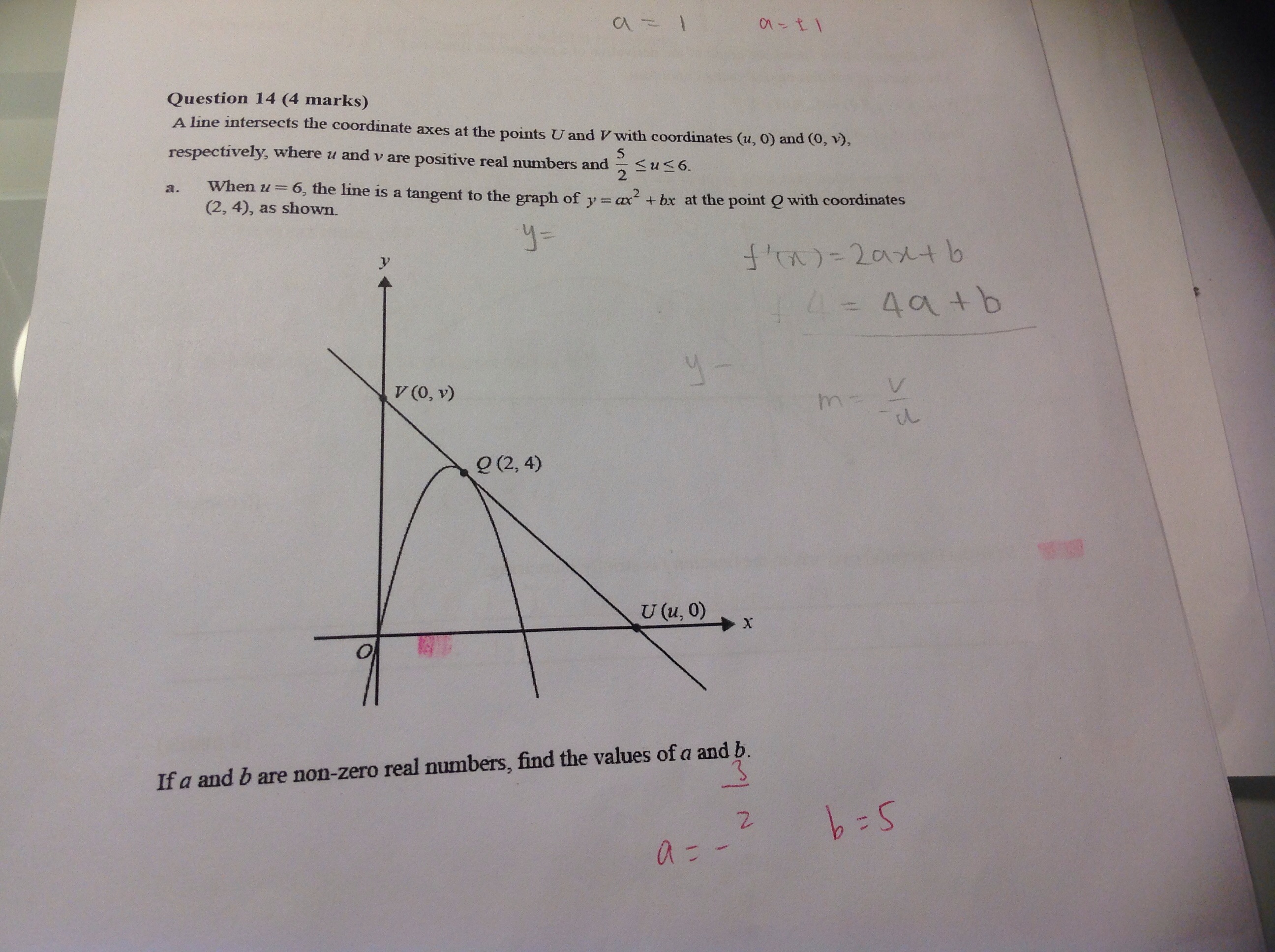
Can someone please explain to me how to do question 14? Thanks!

Answer 1

See below.

Explanation:

The tangent line is given by

`L->p = Q+lambda(U-V)` with `p = (x,y)` and given

`f(p)=y-(ax^2+bx)` we have also

`f(p)=f(Q+lambda(U-V))=0` or solving for `lambda`

`lambda = (4 a u + b u + v pm sqrt[8 a u (2 u + v) + (b u + v)^2])/(2 a u^2)`

but if `L` is tangent to `f` then

`8 a u (2 u + v) + (b u + v)^2=0`

then solving the system

`{(8 a u (2 u + v) + (b u + v)^2=0),(f(Q)=0):}`

at `u=6` we obtain

`a = -1/12 (12 +v), b = (24 + v)/6`

but

`-u/v = -6/v = dy/dx` at `Q` then

`-6/v = 2a x+b=4a+b` and then solving

`{(a = -1/12 (12 +v)),(b = (24 + v)/6),(-6/v=4a+b):}`

we get the solution.

Answer 2

Please see below.

Explanation:

`y = ax^2+bx`

From the fact that #(2,4) lies on the parabola, we get

`4 = a(2)^2+b(2)`, so

`color(blue)(2a+b=2)` `" "` eq (1)

The slope of the tangent line can be found in two ways

Using the definiton of the slope of the tangent line (the derivative) we get:

`dy/dx = 2ax+b`

So at `x=2`, we have `m = 4a+b`

AND

we can find the slope using the two points `(2,4)` and `(6,0)`

`m = (0-4)/(6-2) = -1`

This gives us

`color(blue)(4a+b=-1)` `" "` eq (2)

Now solve the system formed be eq (1) and eq (2).

`{(2a+b=2),(4a+b=-1) :}`

Subtracting the first from the second gets us:

`2a = -3`, so `a = (-3)/2`

And the first equation now gets us `2((-3)/2)+b = 2` so

`-3+b = 2` and `b = 5`.