How to solve these questions steps by steps ?
The diagram below shows a straight line graph obtained by plotting #log_10 y# against x. The variables x and y are related by the equation #y = (2w )/ 3 ^ x# , where w is a constant.
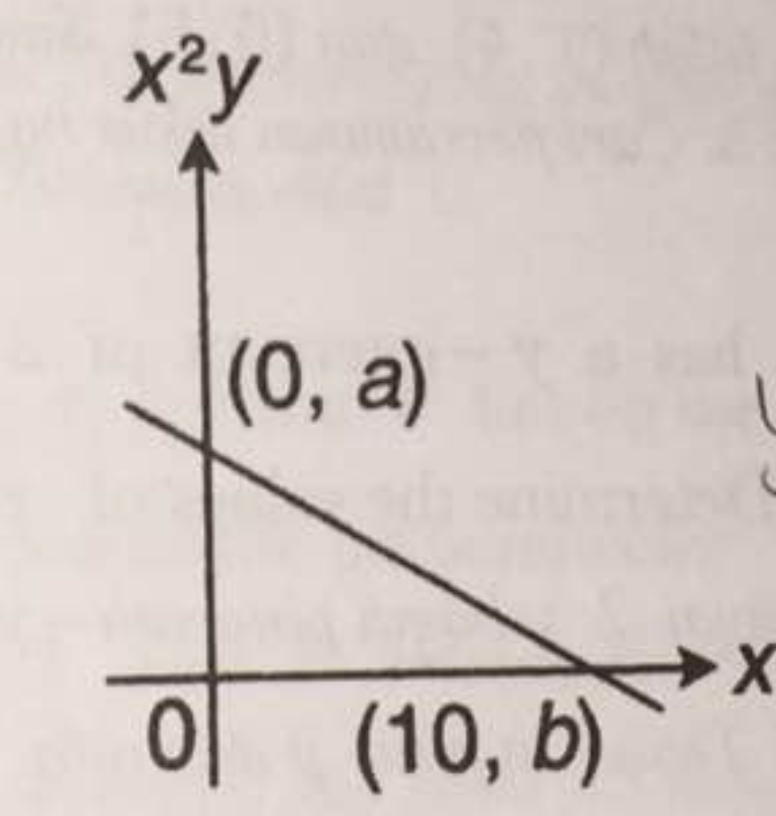
a) Express the equation #y = (2w) / 3 ^ x# in the linear form, used to obtain the straight line graph as shown in the figure above.
b) Find the value of w.
The diagram below shows a straight line graph obtained by plotting
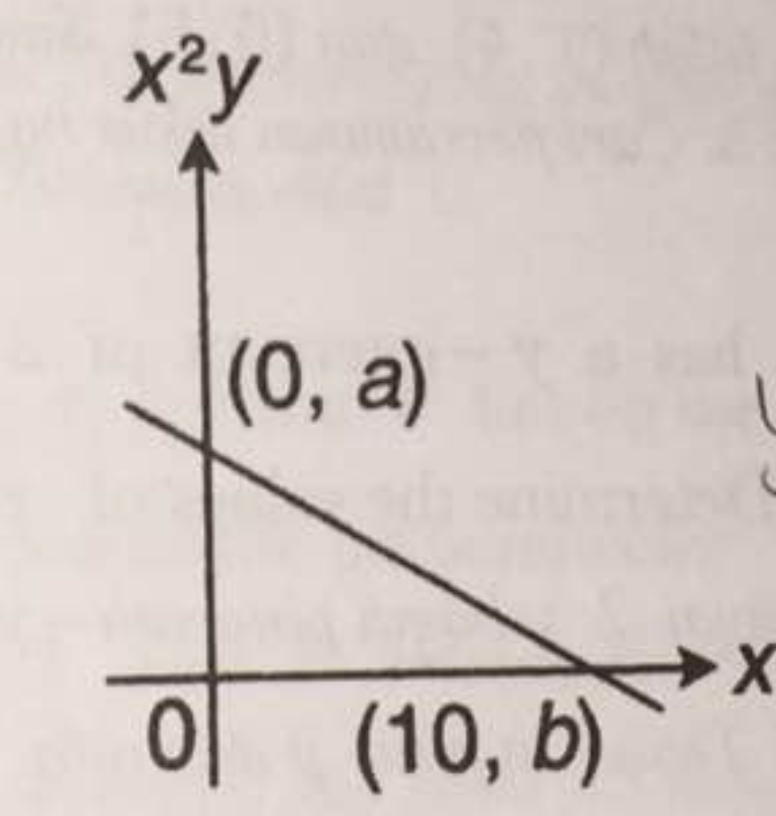
a) Express the equation
b) Find the value of w.
1 Answer
# log_10 y = - (log_10 3)x + log_10 (2w) #
# :. w = (log_10 3^5)/(1-1/3^10) ~~ 2.39#
Explanation:
Note that the question indicates that the diagram shows a straight line graph obtained by plotting
We have:
# y = (2w) / 3^x #
Part (A):
Taking base 10 logarithms of the given equation, we get:
# log_10 y = log_10 {(2w) / 3^x} #
# \ \ \ \ \ \ \ \ \ \ = log_10 (2w) -log _10(3^x) #
# \ \ \ \ \ \ \ \ \ \ = log_10 (2w) -x log_10 3 #
# :. log_10 y = - (log_10 3)x + log_10 (2w) #
Which is in the form,
# Y = mX + c #
which, is that of a straight line.
Part (B):
Given (from the graph) that the straight line passes through the coordinate
# :. log_10 a = 0 + log_10 (2w) #
# :. a = 2w #
Given (from the graph) that the straight line passes through the coordinate
# :. log_10 b = - (log_10 3)10 + log_10 (2w) #
# :. log_10 b = log_10 (2w) - (log_10 3^10) #
# :. b = (2w)/3^10 #
We can also evaluate the gradient of the line:
# m = (Delta Y)/(Delta X) = (b-a) / (10-0)#
So therefore:
# -log_10 3 = ((2w)/3^10-2w)/10#
# :. -log_10 3 = 2w((1/3^10-1)/10) #
# :. w((1-1/3^10)/5) = log_10 3 #
# :. w(1-1/3^10) = 5log_10 3 #
# :. w = (log_10 3^5)/(1-1/3^10) ~~ 2.39#

