How to solve this problem step by step with application of integration?
3 Answers
Explanation:
First, let's find the
For
For
In order to calculate the requested area, our definite integral must then be evaluated in the interval
We can do this by halving the interval; by adding the area under
First, let's evaluate the indefinite integrals for each line:
and
Then, let's evaluate these integrals at the bounds mentioned earlier:
and
Finally, the area is the sum of these two values:
The answer is
Explanation:
So I'm gonna assume you don't know anything about integration.
The region is bounded by
First you need to find where the two lines cut the X-axis, you do that by replacing the
I really do hope i don't have to go any further then this, but if necessary i will help, I'm just having a bit of trouble with writing out the formulas.
Explanation:
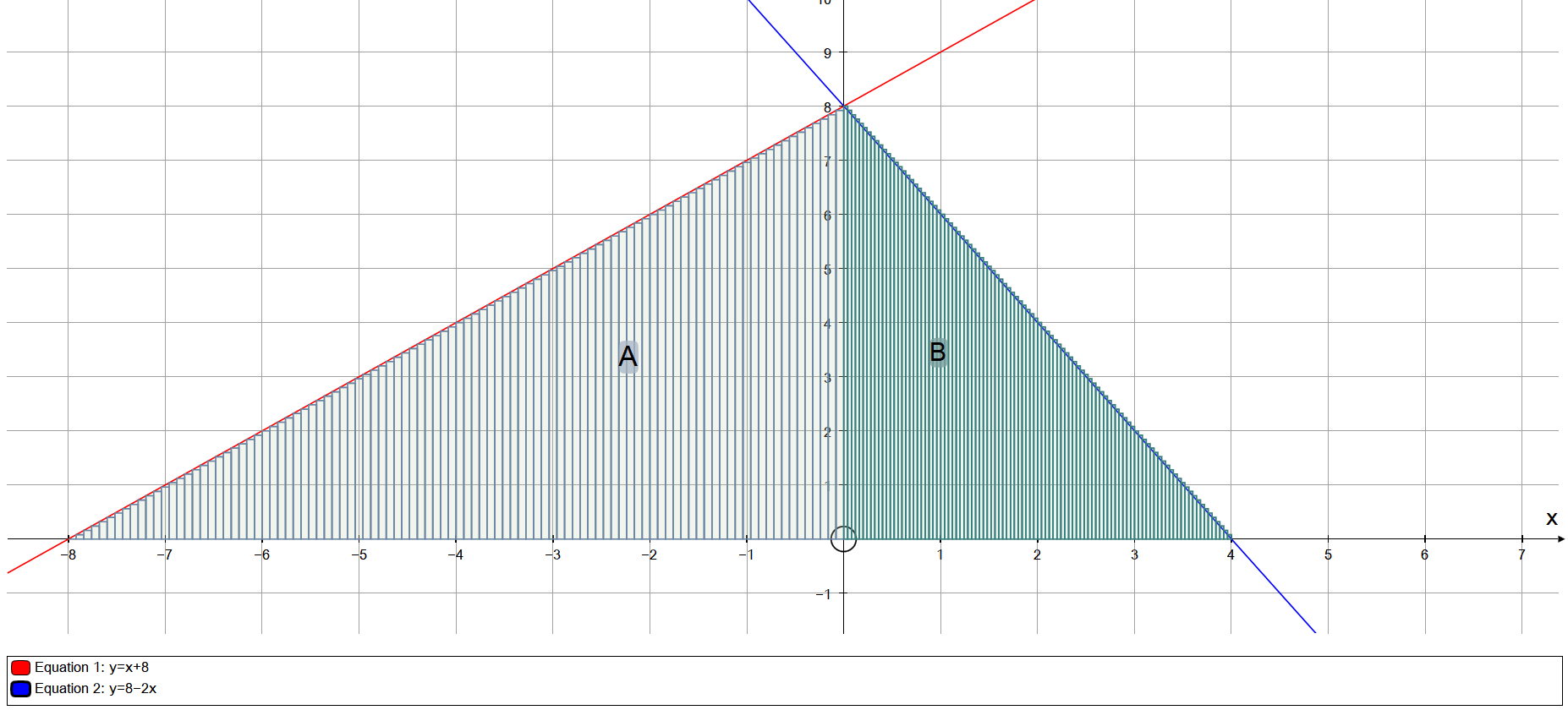
We can calculate the given area by finding Area A and area B and adding these to find total area.
To find area A we need the upper and lower bounds. We can see where these are from the graph, but it is always best to find them algebraically, graphs are not normally accurate enough.
These can be found by solving:
Our upper bound is at the y axis,
So we need the integral:
Area
Plugging in upper and lower bounds:
Area
Area
For area B
The upper bound is:
So we need integral:
Area
Plugging in upper and lower bounds:
Area
Area
Total area:



