How to solve this variable acceleration Q, parts a to c?

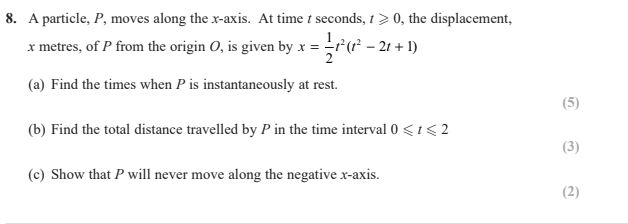
enter image source here

thank you

1 Answer
Ananda Dasgupta
Jun 8, 2018

a) #t=0#, #t=1/2# and #t =1#.
b) #33/16#
c) see below

Explanation:

The expression for the position can be rewritten in the form :
#x = 1/2 t^2(t-1)^2#

a) The velocity is

#v = dx/dt = t(t-1)^2+t^2(t-1)#
#quad = t(t-1)(2t-1)#

Thus the particle is at rest (#v=0#) at the times #t=0#, #t=1/2# and #t =1#.

b) Since the velocity, which in this case is a continuous function, vanishes at #t=0#, #t=1/2# and #t = 1#, it must change sign at this points. So, to calculate the distance traveled, we must consider each of these time intervals separately. Now

  • displacement between #t=0# and #t = 1/2# :
    #x(1/2)-x(0) = 1/2times (1/2)^2(1/2-1)^2-0#
    #qquad = 1/32#
  • displacement between #t=1/2# and #t = 1# :
    #x(1)-x(1/2) = 0-1/2times (1/2)^2(1/2-1)^2#
    #qquad = -1/32#
  • displacement between #t=1# and #t = 2# :
    #x(2)-x(1) = 1/2times (2)^2(2-1)^2-0#
    #qquad = 2#

The distances traveled in these three intervals are #1/32#, #1/32# and #2# respectively.

Thus the total distance traveled is #1/32+1/32+2 = 33/16#

c) It is easy to see that #1/2t^2(t-1)^2# can never be negative.

Related questions
Impact of this question
1202 views around the world
You can reuse this answer
Creative Commons License