How to write the statement #S_1,S_2,S_3#? Thanks!
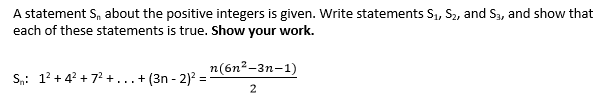
1 Answer
We have:
# S_n: 1^2 + 4^2 + 7^2 + ... (3n-2)^2 = (n(6n^2-3n-1))/2 #
So then statements
# S_1: 1^2 = (1(6-3-1))/2 #
# \ \ \ \ \ \ => 1 = 2/2 = 1 # , which is true .
# S_2: 1^2 +4^2= (2(24-6-1))/2 #
# \ \ \ \ \ \ => 1+16 = 18-1# , which is also true .
# S_3: 1^2 +4^2 + 7^2= (3(54-9-1))/2 #
# \ \ \ \ \ \ => 1+16 +49 = 66# , which is also true .
In general, we can prove the result is true using Induction:
Induction Proof - Hypothesis
We seek to prove that:
# sum_(k=1)^n \ (3k-2)^2 = (n(6n^2-3n-1))/2 # ..... [A]
So let us test this assertion using Mathematical Induction:
Induction Proof - Base case:
We will show that the given result, [A], holds for
When
So the given result is true when
Induction Proof - General Case
Now, Let us assume that the given result [A] is true when
# sum_(k=1)^m \ (3k-2)^2 = (m(6m^2-3m-1))/2 # ..... [B]
Consider the LHS of [A] with the addition of the next term, in which case we have
# LHS = sum_(k=1)^(m+1) \ (3k-2)^2 #
# \ \ \ \ \ \ \ \ = {sum_(k=1)^m \ (3k-2)^2 } + (3(m+1)-2)^2 #
# \ \ \ \ \ \ \ \ = (m(6m^2-3m-1))/2 + (3m+1)^2 \ \ \ # using [B]
# \ \ \ \ \ \ \ \ = (m(6m^2-3m-1) + 2(3m+1)^2)/3 #
# \ \ \ \ \ \ \ \ = (6m^3-3m^2-m + 2(9m^2+6m+1))/2 #
# \ \ \ \ \ \ \ \ = (6m^3-3m^2-m + 18m^2+12m+2)/2 #
# \ \ \ \ \ \ \ \ = (6m^3+ 15m^2+11m+2)/2 #
# \ \ \ \ \ \ \ \ = ((m+1)(6m^2+9m+2))/2 #
# \ \ \ \ \ \ \ \ = ((m+1)(6(m^2+2m+1)-12m-6+9m+2))/2 #
# \ \ \ \ \ \ \ \ = ((m+1)(6(m+1)^2-3m-4))/2 #
# \ \ \ \ \ \ \ \ = ((m+1)(6(m+1)^2-3(m+1)-1))/2 #
Which is the given result [A] with
Induction Proof - Summary
So, we have shown that if the given result [A] is true for
Induction Proof - Conclusion
Then, by the process of mathematical induction the given result [A] is true for
Hence we have:
# sum_(k=1)^n \ (3k-2)^2 = (n(6n^2-3n-1))/2 \ \ \ QED#

