Question

How was the formula for the area of a kite created?

Answer 1

Decompose a kite into two triangles and take the sum of the areas of the triangles

Explanation:

Consider the diagram below of a kite with diagonals of length `d` and `w`:

`bar(color(white)("XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX")`

`triangle ABD` has an area `=("base" xx "height")/2`

`color(white)("XXXXXXXXXXXXX")=(wx)/2`

`bar(color(white)("XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX")`

`triangle BCD` has an area `=("base" xx "height")/2`

`color(white)("XXXXXXXXXXXXX")=(w xx (d-x))/2 = (wd)/2-(wx)/2`

`bar(color(white)("XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX")`

`"Area of kite"`
`color(white)("XXX")=Area_"ABD" + Area_"BCD"`

`color(white)("XXX")= ((wx)/2) + ((wd)/2 - (wx)/2)`

`color(white)("XXX")=(wd)/2`

Answer 2

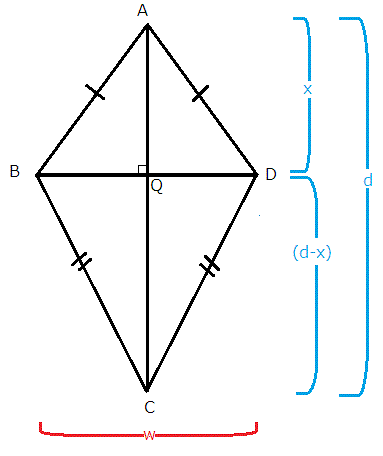
Here are a couple more images that might make the derivation of the formula for the area of a kite more intuitively obvious.

Explanation:

The kite deformed into a triangle:

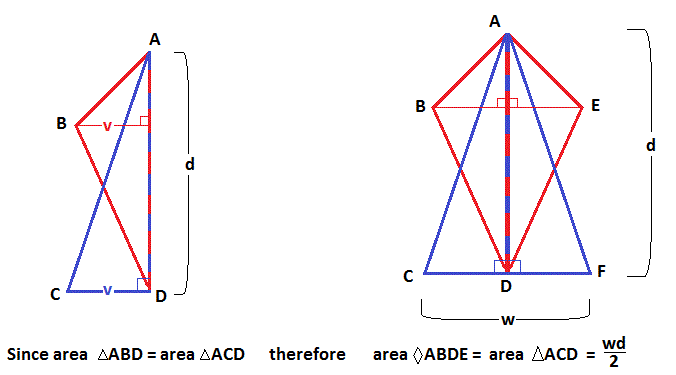
The kite embedded in a rectangle:

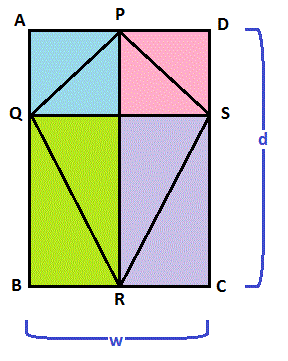
Segments of the kite occupy `1/2` of each quadrant of the rectangle (and thus has an area `= 1/2 xx` area of the rectangle).

Note that this second image implies that any convex quadrilateral with perpendicular diagonals (of which a kite is an example) has the same formula for its area.