Question

How will you draw a square equal in area to a given triangle?

Answer 1

See below.

Explanation:

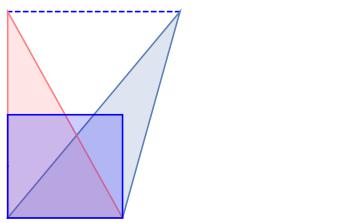
Given the triangle `ABC` (light blue) we construct the equivalent area triangle `ABC'` (pink) by sliding the tip `C` parallel to the basis `AB` forming the rectangular triangle `ABC'`

After that we construct the equivalent area quadrilateral `ABDE` (blue) with sides `bar(AB)` and `1/2 bar(AC')` and with the same area as triangle `ABC`

Now we need a square with side `L` such that `L^2= bar(AB) xx 1/2 bar(AC')`

and this is done drawing a circumference with origin at `1/2(bar(AB) + 1/2 bar(AC'))` and radius `r = 1/2(bar(AB) + 1/2 bar(AC'))` and drawing a perpendicular line to the diameter issuing from the point `(bar(AB),0)` and intersecting the circumference at `(bar(AB),F)`. Now the distance from `F` to the perpendicular foot is `L`.

Answer 2

Find the area of the triangle and then find the square root find the length of the sides of the square.

Explanation:

Assuming that you have all the measurements of the given triangle, you can calculate the area:

`A = 1/2bh`

If you do not have the measurements, but a scale drawing, you can measure the length of the base and the height.

Once you have the area of the triangle, you also have the area of the square,

To find the length of the side:

`s xx s = A`

`s^2 = A`

`s = sqrtA`

Find the square root of the area to find the length of the sides of the square.

Use this length to draw a square,

This is by calculation, rather than by construction.

Answer 3

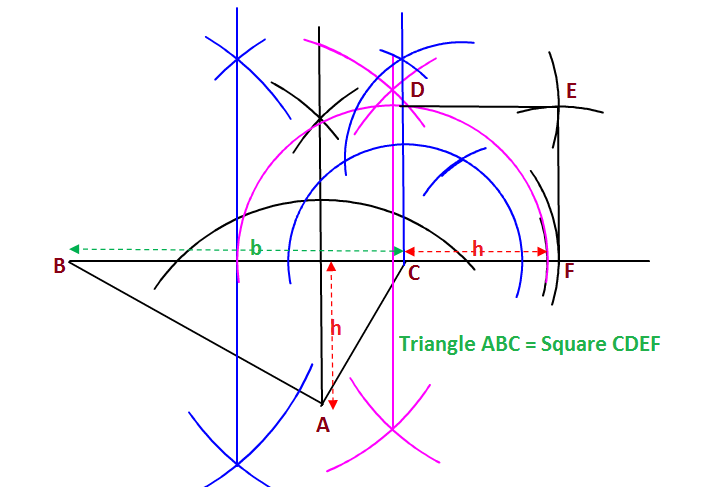
Steps

1. The base `BC=b` of the given `DeltaABC` is bisected
2. Perpendicular `h` from A to `BC` is drawn.
3. line segment of length `h` is cut off from the extended part of `BC`
4. Line segment of length `b/2+h` is bisected and a semicircle is drawn taking `b/2+h` as diameter
5. Perpendicular `CD` on `BC` is drawn , which intersects semicircle at `D`. Now the length of `CD` will be mean proportion of `b/2 and h`. Hence `CD^2=1/2xxbxxh="Area of "Delta ABC`
6. So a square `CDEF` completed on side `CD` is the required square.