Question

How will you prove that work done in isothermal process is always greater than adiabatic process?

Answer 1

I assume you mean for an ideal gas. It is much harder for a real gas...

---

We will focus on reversible work, because it is the maximum work that can be done. It is the only fair comparison, because there are an infinity of combinations of irreversible work paths.

The isothermal and adiabatic ideal gas equations of state are, respectively`""^(‡)`:

`PV = "const"`

`PV^gamma = "const"`, `" "` `gamma = barC_P/barC_V = (barC_V + R)/(barC_V) = 1 + R/(barC_V)`

`""^(‡)`The full derivation for the `PV` expressions is shown here!

To compare the PV work quantities, we examine the slope, `(dP)/(dV)` in both scenarios. The reversible work is the area under the curve of a PV graph, so the steeper slope would give a smaller amount of work for the same `DeltaV`.

From the differential forms:

Isothermal:

`d(PV) = PdV + VdP = 0`

`=>` `color(blue)(barul|stackrel(" ")(" "((delP)/(delV))_T = -P/V" ")|)`

Adiabatic:

`d(PV^gamma) = P cdot d(V^gamma) + V^gamma dP`

`= P cdot gammaV^(gamma-1)dV + V^gamma dP = 0`
(where we had used the chain rule on the first term to recover `dV`)

Dividing through by `V^gamma` gives:

`=> gammaP/VdV + dP = 0`

`=> dP = -gammaP/VdV`

As a result, for an adiabatic process,

`color(blue)(barul|stackrel(" ")(" "((delP)/(delV))_q = -gamma P/V " ")|)`

Here we have a `gamma` term that is always greater than `1`.

This tells us that if the gas is doing isothermal work, the slope is generally less steep. Therefore, the work done (the area under the PV curve) is typically bigger.

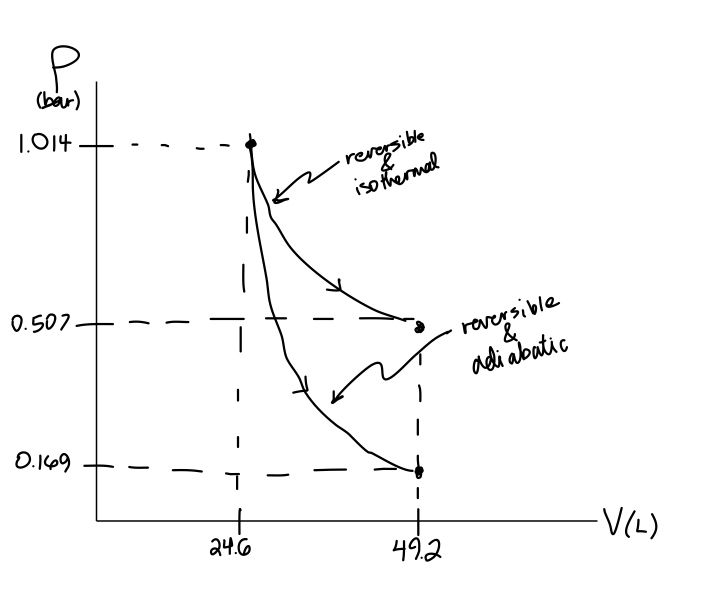
Here is a graph from a problem I did in Levine:

If the gas is expanding, it follows the curve downwards. If the gas is compressing, it follows the curve upwards. Either way the area under the curve is the reversible work done.