Question

How would I write `-4x^2 + 9y^2 + 32x + 36y - 64 = 0` in standard form? What are the steps?

Answer 1

`-4x^2 + 9y^2 + 32x + 36y - 64 = 0` is in the General Cartesian Form of a Conic Section

`Ax^2+Bxy + Cy^2+Dx +Ey + F = 0`

One should use the Discriminant:

`Delta = B^2-4AC`

to determine which conic section the equation describes.

If `Delta < 0`, then it is a circle or an ellipse. If `B = 0` and `A=C` then it is a circle. Otherwise, it is an ellipse.

If `Delta = 0`, then it is a parabola.

If `Delta > 0`, then it is a hyperbola and, if `A+C = 0`, then it is a square hyperbola.

We observe that `A = -4, B = 0, and C = 9`:

`Delta = 0^2-4(-4)(9) = 144`, therefore, it is a hyperbola.

There are two standard forms for a hyperbola.

1 The horizontal transverse axis form:

`(x-h)^2/a^2-(y-k)^2/b^2=1`

2 The vertical transverse axis form:

`(y-k)^2/a^2-(x-h)^2/b^2=1`

If either case, we need to make the equation fit the patterns:

`(x - h)^2 = x^2-2hx+h^2` and `(y - k)^2= y^2-2ky +k^2`

then one of the two forms will follow.

Returning to the equation:

`-4x^2 + 9y^2 + 32x + 36y - 64 = 0`

Add 64 to both sides and group the x terms and y terms together:

`-4x^2 + 32x + 9y^2 + 36y = 64`

Please observe that the coefficient of the `x^2` term is -4; this means that we need to multiply the pattern for the x terms by -4:

`-4(x - h)^2 = -4x^2+8hx-4h^2`

This tells us that we must subtract `4h^2` from both sides of the equation:

`-4x^2 + 32x-4h^2 + 9y^2 + 36y = 64-4h^2`

We can find the value of h by setting the middle term in the pattern equal to the corresponding term in the equation:

`8hx = 32x`

`h = 4`

We can substitute `-4x^2 + 32x-4h^2= -4(x-4)^2` on the left side and we can substitute `h = 4` on the right:

`-4(x-4)^2 + 9y^2 + 36y = 64-4(4)^2`

Simplify the right side:

`-4(x-4)^2 + 9y^2 + 36y = 0`

Please observe that the coefficient of the `y^2` term is 9; this means that we need to multiply the pattern for the y terms by 9:

`9(y - k)^2= 9y^2-18ky +9k^2`

This tells us that we must add `9k^2` to both sides of the equation:

`-4(x-4)^2 + 9y^2 + 36y +9k^2= 9k^2`

We can find the value of k by setting the middle term in the pattern equal to the corresponding term in the equation:

`-18ky = 36y`

`k = -2`

We can substitute `9y^2 + 36y +9k^2 = 9(y-(-2))^2` on the left and `k = -2` on the right:

`-4(x-4)^2 + 9(y-(-2))^2= 9(-2)^2`

Swap the two terms on the left and simplify the right:

`9(y-(-2))^2-4(x-4)^2 = 36`

Divide both sides of the equation by 36:

`(y-(-2))^2/4-(x-4)^2/9 = 1`

Write the denominators as squares:

`(y-(-2))^2/2^2-(x-4)^2/3^2 = 1`

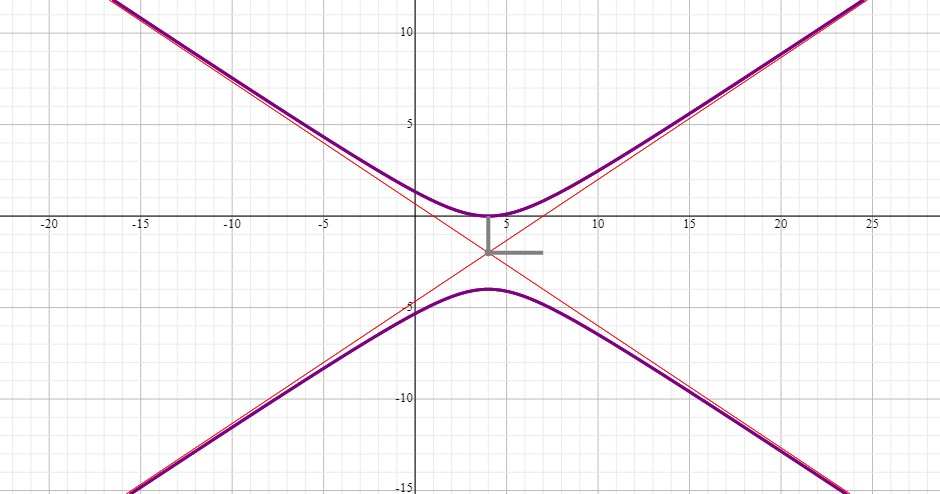
The above is standard form for a hyperbola with a vertical transverse axis.

Answer 2

Please see below.

Explanation:

.

`-4x^2+9y^2+32x+36y-64=0`

First we factor out the coefficient of `x^2` from the `x` terms and coefficient of `y^2` from the `y` terms:

`-4(x^2-8x)+9(y^2+4y)-64=0`

Then we need to complete the square for the `x` and `y` parts by adding and subtracting a constant as such:

`-4(x^2-8x+16-16)+9(y^2+4y+4-4)-64=0`

`-4[(x-4)^2-16]+9[(y+2)^2-4]-64=0`

Now, we multiply the `-4` and `9` through and remove the brackets:

`-4(x-4)^2+64+9(y+2)^2-36-64=0`

After simplifying :

`-4(x-4)^2+9(y+2)^2=36`

Now. we divide the equation by `36`:

`(-4(x-4)^2)/36+(9(y+2)^2)/36=1`

After simplifying, we get:

`(-(x-4)^2)/9+(y+2)^2/4=1`

`(y+2)^2/4-(x-4)^2/9=1`

This is the equation of a hyperbola whose graph can be seen below: