Question

How would you compare diffusion with effusion?

Answer 1

Here's my interpretation.

Explanation:

Diffusion is when a substance disperses evenly throughout a medium; i.e. a perfume dispersing its scent through a room:

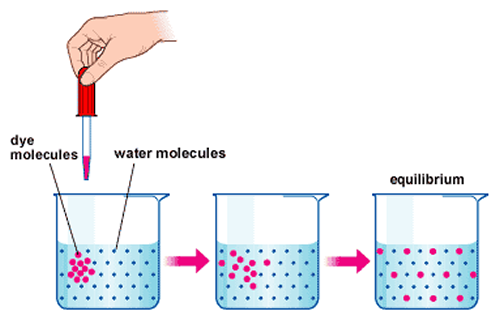
Effusion is when a substance "escapes" through a (tiny) opening; i.e. helium in a balloon escaping through the balloon's rubber network:

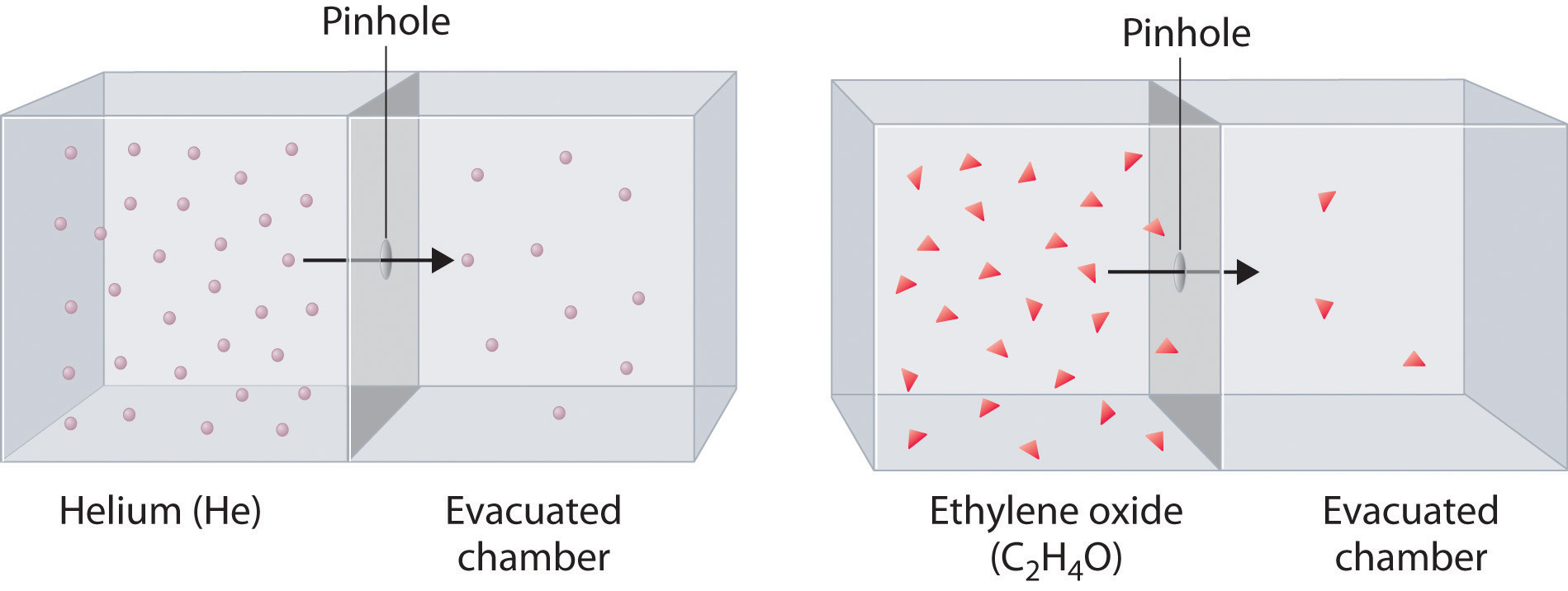
We can infer that the rates of diffusion and effusion of a gas depend on the speed of the particles.

In the effusion image, we notice that `"He"` effuses faster than `"C"_2"H"_4"O"_2`....but why?

Graham's law of effusion (or diffusion) explains this:

`(r_1)/(r_2) = sqrt((M_2)/(M_1))`

where

• `(r_1)/(r_2)` is the ratio of the rates of effusion of a gas 1 and a gas 2

• `M_1` and `M_2` are the molar masses of gases 1 and 2

This equation tells us that

The rate of effusion (and diffusion) of a gas is inversely proportional to the square root of its molar mass.

Therefore, the lower the mass of a gas, the higher its rate of effusion and the higher its speed.

This makes intuitive sense, as a gas with less mass should move faster than a gas with more mass.

In terms of rates and speeds, effusion and diffusion are quite similar.

The difference between the two is that diffusion is the spreading out of a substance within a dispersing medium, and effusion is when a substance escapes through a tiny pinhole, or other hole.

Another way to differentiate between diffusion and effusion is to imagine effusion as motion of particles through a hole one-dimensionally (i.e. `+-x`), and diffusion allows for all three dimensions (i.e. `+-x, +-y, +-z`).

`uarr` Credit Truong-Son N. for this addition `uarr`