Question

How would you evaluate `int_0^pi/2 sqrt(sinx)dx` . ?

Answer 1

Note that there is no real value anti-derivative for `sqrt(sin(x))`. This is easy to see if you consider values of `x` in the 3rd and 4th quadrants where `sin(x)` is negative.

If you really need the value of this integral, here is how I would do it:

Chop the function up into smaller and smaller incremental steps, taking the minimum and maximum valued areas for each rectangular strip; sum the minimum and the maximum areas separately and keep shopping the strips until you get a difference between the minimum and maximum total areas that is within some tolerable limit.

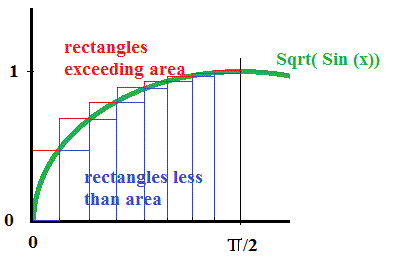
Of course, I'm not going to do this by hand but a simple Basic programs using a error tolerance of 0.0001 gives the result:

Integral value of Sqrt(Sin(x)) for x from 0 to pi/2 falls between 1.1980921 and 1.19818798

(I've omitted the Basic code to keep the size of this answer reasonable, but it is available if you want it).

For an alternate view which claims to provide an exact solution method (although I haven't been able to work through the details), see: http://www.enotes.com/homework-help/integration-sqrt-sin-x-346600