How would you solve the following using a table? Andrew cashes a $180 check and wants the money in $10 and $20 bills. The bank teller gives him 12 bills. How many of each kind of bill does he receive?
1 Answer
We can solve this problem using a table and a pair of linear equations.
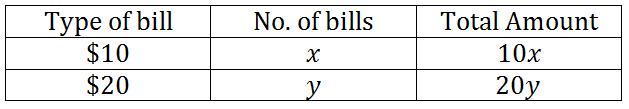
(The dollar sign has been disregarded.)
Now, we know that he has received a total amount of $180. Thus, our first equation is:
Now, we need another equation. We know that he has received 12 bills in total. Therefore, our second equation is:
To make at least one variable term exactly like in the first equation, I will multiply this equation by 10, getting:
Subtracting equation (2) from (1),
Therefore,
Substituting
Thus, we can conclude that he receives 6 bills each of $10 and $20.
