How would you solve this equation?

2 Answers
Explanation:
Since cos can have a value between -1 & +1 only, 4 is not a valid solution.
Cosine is negative in II and III Quadrant.
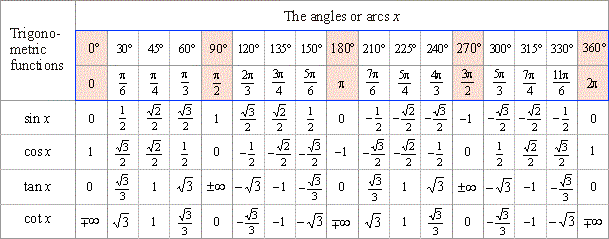
Explanation:
This will be a piece of cake if you just assume a variable equal to
So, Let's Assume
Now the Equation is,
So, Either
Or,
So,
Now,
Cosine (
So,
Now,
Hope this helps.

