I'm trying to find the real zeros and put it in factored form, but I can't get it right. A\N is f(x) = (x-1)(3x-1)(x-i)(x+i). How do I get (3x-1)?
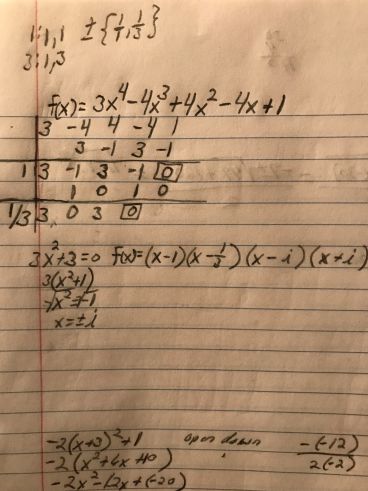
2 Answers
The first two terms are correct. Then, you got
This then becomes
The two answers are the same:
Though the one without the fraction is the conventional way to present the root.
Explanation:
In terms of a solution of the zeros of a function, the factors
or
The way to think about how to get one from the other is to think about multiplying both sides by a common factor. Since one side of the equation is zero, it has no effect overall.


