Question

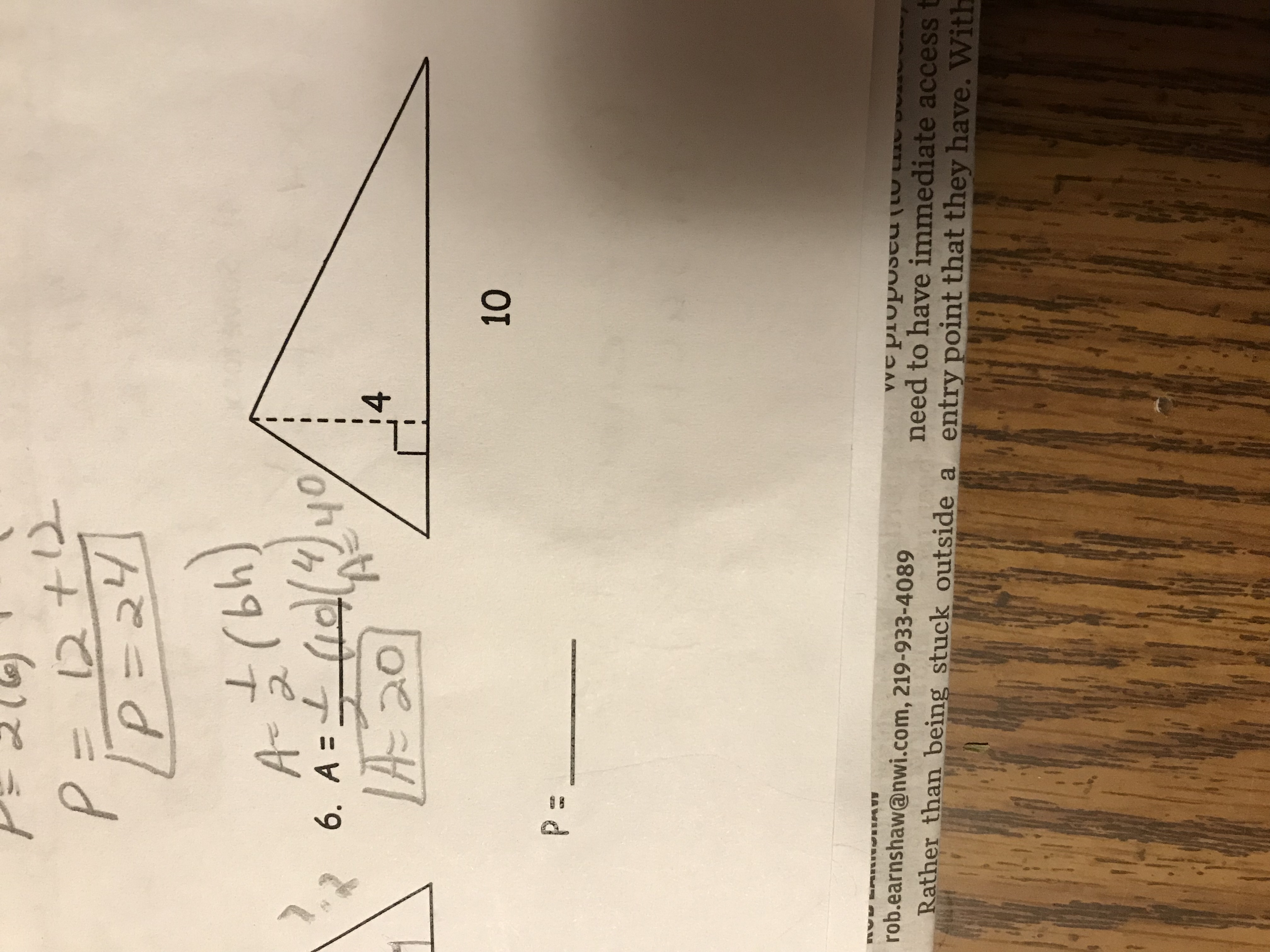
I need to find the perimeter of this triangle. I already found the area. How do I find the lengths of the other sides?

Answer 1

The perimeter cannot be determined without more information regarding the shape of the triangle.

Explanation:

This is a reference to Heron's formula. I shall be using the form allows one to compute the area of a triangle given the length of the 3 sides:

`A = 1/4sqrt(4(a^2b^2+a^2c^2+b^2c^2)-(a^2+b^2+c^2)^2)`

Given: `b = 10` and `A = 20`:

`20 = 1/4sqrt(4(100a^2+a^2c^2+100c^2)-(a^2+100+c^2)^2)`

Multiply both sides by 4:

`80 = sqrt(4(100a^2+a^2c^2+100c^2)-(a^2+100+c^2)^2)`

Because the area must be a positive number, squaring both sides will not introduce any extraneous roots:

`6400= 4(100a^2+a^2c^2+100c^2)-(a^2+100+c^2)^2`

Expand the square and distribute the 4:

#6400= 400a^2+4a^2c^2+400c^2-(a^4 + 2 a^2 c^2 + 200 a^2 + c^4 + 200 c^2 + 10000 )" [1]"#

Let `x =` the base of the small right triangle, `10-x` be the base of the large right triangle, and use the Pythagorean theorem to with the lengths of sides `a` and `c` in terms of x:

`a^2=4^2+x^2`

`a^2=x^2+16" [2]"`

`c^2 = 4^2+ (10-x)^2`

`c^2 = x^2-20x+116" [3]"`

Substitute equations [2] and [3] into equation [1]:

#6400= 400(x^2+16)+4(x^2+16)(x^2-20x+116)+400(x^2-20x+116)-((x^2+16)^2 + 2 (x^2+16)(x^2-20x+116) + 200(x^2+16) + (x^2-20x+116)^2 + 200(x^2-20x+116) + 10000 )#

I must have made an error the first time that I entered this equation into WolframAlpha.

The first time that I did this, I obtained 2 pairs of complex conjugate roots but I have done this attempt more formally. If you open the link in a separate tab or window, you will see that the computation engine says that the equation is true for all values of x. This is a much stronger proof that there is no unique solution for the perimeter given only the base and the height.