I really don't understand this calculus 2 problem?
The question is: An equilateral hexagon is revolving around one of its edges. Find the volume of the solid of revolution
The question is: An equilateral hexagon is revolving around one of its edges. Find the volume of the solid of revolution
3 Answers
Apr 29, 2017
Explanation:
Considering
we have
but
Apr 30, 2017
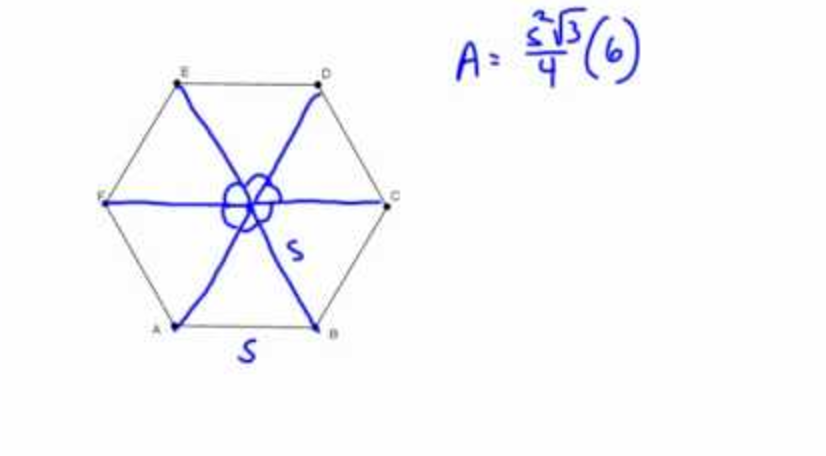
Pappus 2nd Theorem: Volume V of a solid of revolution generated by rotating a plane figure about an external axis is equal to the area of the figure times the distance traveled by its geometric centroid, or
May 1, 2017
I have solved this way, using integrals, as shown below:



