I really need help. It's about number theory. Would yo be so kind help me?
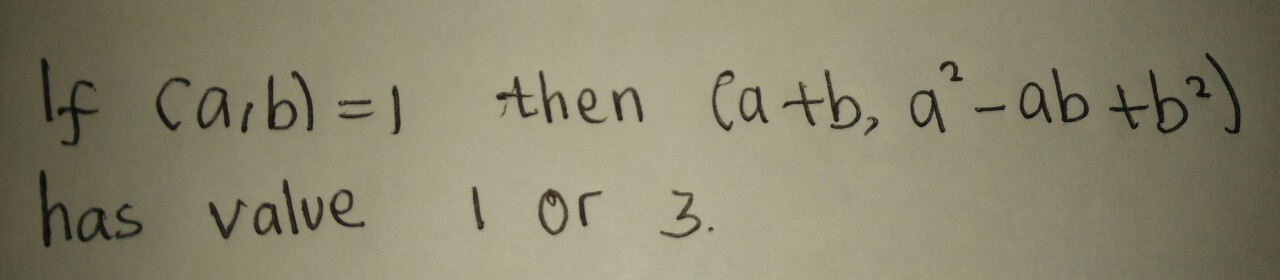
2 Answers
Mar 21, 2018
Use the fact that if
Explanation:
Suppose that
From
Therefore,
Now show that if
Finish by showing that
Mar 22, 2018
See below.
Explanation:
Note that
and also
hence


