Question

If 1.000g of tin metal reacts with 0.640g of fluorine gas, what is the empirical formula of the product?

Answer 1

`"SnF"_4`

Explanation:

The empirical formula of a given compound tells you the smallest whole number ratio in which its constituent elements combine to form said compound.

In your case, an unknown compound is said to contain tin, `"Sn"`, and fluorine, `"F"`. This compound is synthesized by reacting tin metal with fluorine gas, `"F"_2`.

It's important to realize that fluorine gas exists as diatomic molecules, and so its molar mass will be twice as big as the molar mass of fluorine, `"F"`.

Grab a periodic table and look for tin and fluorine. Their molar masses are

`M_("M Sn") = "118.72 g mol"^(-1)`

`M_("M F") = "18.998 g mol"^(-1)`

The molar mass of fluorine gas will thus be

`M_("M F"_ 2) = 2 xx M_("M F")`

`M_("M F"_ 2) = 2 xx "18.998 g mol"^(-1) = "37.996 g mol"^(-1)`

This means that your sample of fluorine gas contained

`0.640 color(red)(cancel(color(black)("g"))) * "1 mole F"_2/(37.996color(red)(cancel(color(black)("g")))) = "0.016844 moles F"_2`

Since every molecule of `"F"_2` contains `2` atoms of `"F"`

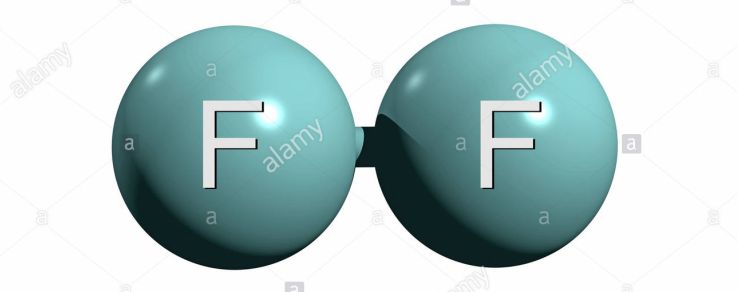
you know that your unknown compound will contain

`0.016844 color(red)(cancel(color(black)("moles F"_2))) * "2 moles F"/(1color(red)(cancel(color(black)("mole F"_2)))) = "0.033688 moles F"`

The sample will also contain

`1.000 color(red)(cancel(color(black)("g"))) * "1 mole Sn"/(118.72 color(red)(cancel(color(black)("g")))) = "0.0084232 moles Sn"`

To find the mole ratio that exists between the two elements in the unknown compound, divide both values by the smallest one

`"For Sn: " (0.0084232 color(red)(cancel(color(black)("moles"))))/(0.0084232color(red)(cancel(color(black)("moles")))) = 1`

`"For F: " (0.033688color(red)(cancel(color(black)("moles"))))/(0.0084232color(red)(cancel(color(black)("moles")))) = 3.999 ~~ 4`

Since `1:4` is already the smallest whole number ratio that can exist here, you can say that this compound has the empirical formula

`"Sn"_1"F"_4 implies color(green)(|bar(ul(color(white)(a/a)color(black)("SnF"_4)color(white)(a/a)|)))`