If #A = <3 ,-1 ,8 >#, #B = <4 ,-3 ,-1 ># and #C=A-B#, what is the angle between A and C?

Question

1405 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-22T13:02:28

#36.22^o# **(2,d.p.)

A= #((3),(-1),(8))#

B= #((4),(-3),(-1))#

C= A - B: C= #((3),(-1),(8))-((4),(-3),(-1))=((-1),(2),(7))#

Angle between A and C:

#((3),(-1),(8))*((-1),(2),(7))#

This is called the Dot product, Scaler product or Inner product and is defined as:

#a*b= |a|*|b|cos(theta)#

#|A|= sqrt(3^2+(-1)^2+8^2)= sqrt(74)#

#|C|= sqrt((-1)^2+2^2+7^2)= sqrt(54)=3sqrt(6)#

#A*C= ((3),(-1),(8))*((-1),(2),(7))=((-3),(-2),(56))#

We need to sum the components in the product vector, so:

#-2-3+56=51#

So now we have:

#51 = sqrt(74)*3sqrt(6)cos(theta)=51/(sqrt(74)*3sqrt(6))= cos(theta)#

#-> 51/(3sqrt(444))=cos(theta)#

#theta= arccos(51/(3sqrt(444))) =36.22^o# (2,d.p.)

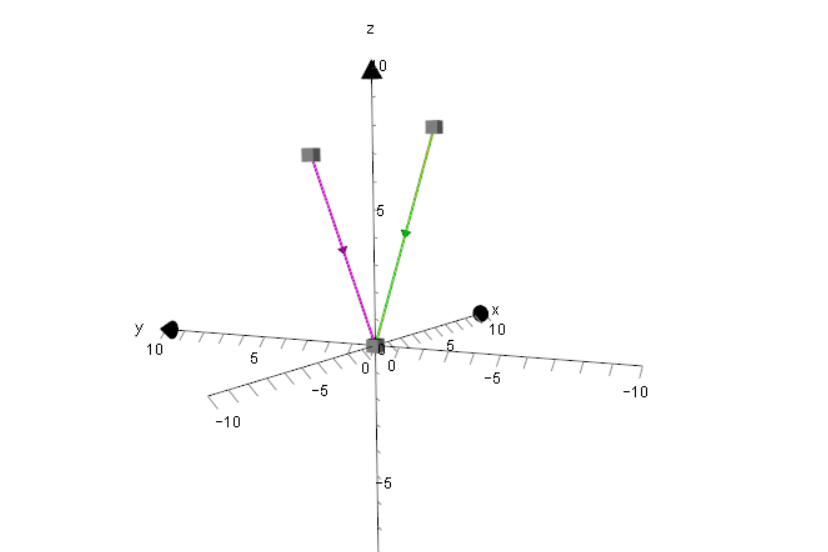
enter image source here

The angle is formed where the vectors are moving in the same relative direction. i.e where both arrow heads are pointing.