Question

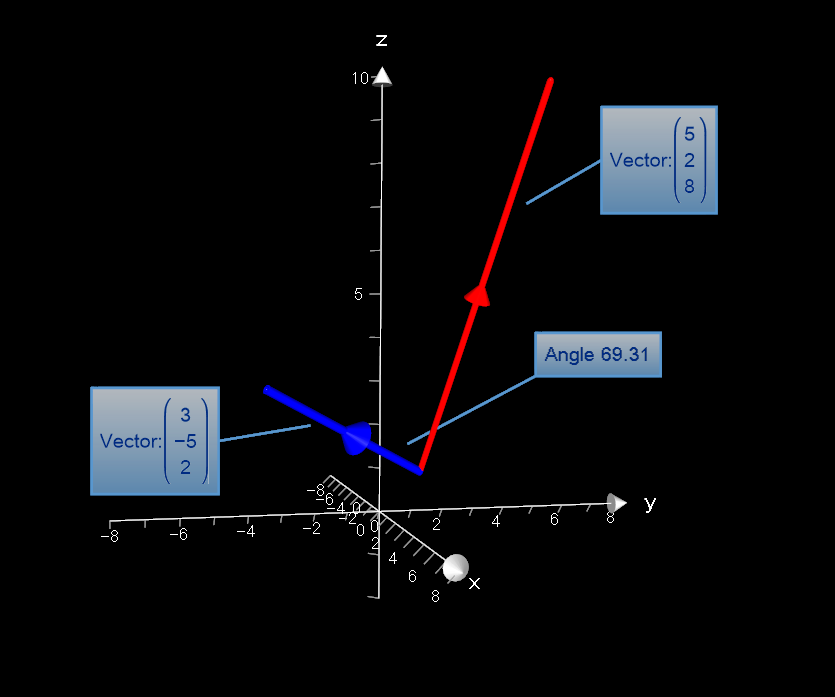
If `A = <5 ,2 ,8 >`, `B = <2 ,7 ,6 >` and `C=A-B`, what is the angle between A and C?

Answer 1

The angle is `=69.3^@`

Explanation:

Start by calculating

`vecC=vecA-vecB`

`vecC=〈5,2,8〉-〈2,7,6〉=〈3,-5,2〉`

The angle between `vecA` and `vecC` is given by the dot product definition.

`vecA.vecC=∥vecA∥*∥vecC∥costheta`

Where `theta` is the angle between `vecA` and `vecC`

The dot product is

`vecA.vecC=〈5,2,8〉.〈3,-5,2〉=15-10+16=21`

The modulus of `vecA`= `∥〈5,2,8〉∥=sqrt(25+4+64)=sqrt93`

The modulus of `vecC`= `∥〈3,-5,2〉∥=sqrt(9+25+4)=sqrt38`

So,

`costheta=(vecA.vecC)/(∥vecA∥*∥vecC∥)=21/(sqrt93*sqrt38)=0.35`

`theta=arccos(0.35)=69.3^@`

Answer 2

`color(blue)(69.31^@` 2 d.p.

Explanation:

`bbA=[(5),(2),(8)] \ \ \ \ \ bbB=[(2),(7),(6)]`

`bbC=bbA-bbB=[(5),(2),(8)]-[(2),(7),(6)]=[(5-2),(2-7),(8-6)]=[(3),(-5),(2)]`

The angle between two vectors can be found using the Dot Product.

`bba*bb(b)=||bba||*||bb(b)||*cos(theta)`

`cos(theta)=(bba*bb(b))/(||bba||*||bb(b)||)`

We first find the magnitudes of `bbA and bb(B)`

This is given by the Distance Formula:

`||bbv||=sqrt((v_1)^2+(v_2)^2+(v_3)^2)`

Where `v_1,v_2,v_3` are the components of the vector.

`||bbA||=sqrt((5)^2+(2)^2+(8)^2)=sqrt(93)`

`||bbC||=sqrt((3)^2+(-5)^2+(2)^2)=sqrt(38)`

Now the product of:

`bbA*bbC`

This is found by multiplying:

`[(5),(2),(8)]*[(3),(-5),(2)]`

For this we multiply corresponding components and the n sum these:

`[(5),(2),(8)]*[(3),(-5),(2)]=[(5*3+2*-5+8*2)]=21`

Using:

`cos(theta)=(bba*bb(b))/(||bba||*||bb(b)||)`

`cos(theta)=(bbA*bbC)/(||bbA||*||bbC||)`

`cos(theta)=21/(sqrt(93)*sqrt(38))`

`theta=arccos(21/(sqrt(93)*sqrt(38)))~~69.313579120997`

`color(blue)(69.31^@` 2 d.p.

PLOT: