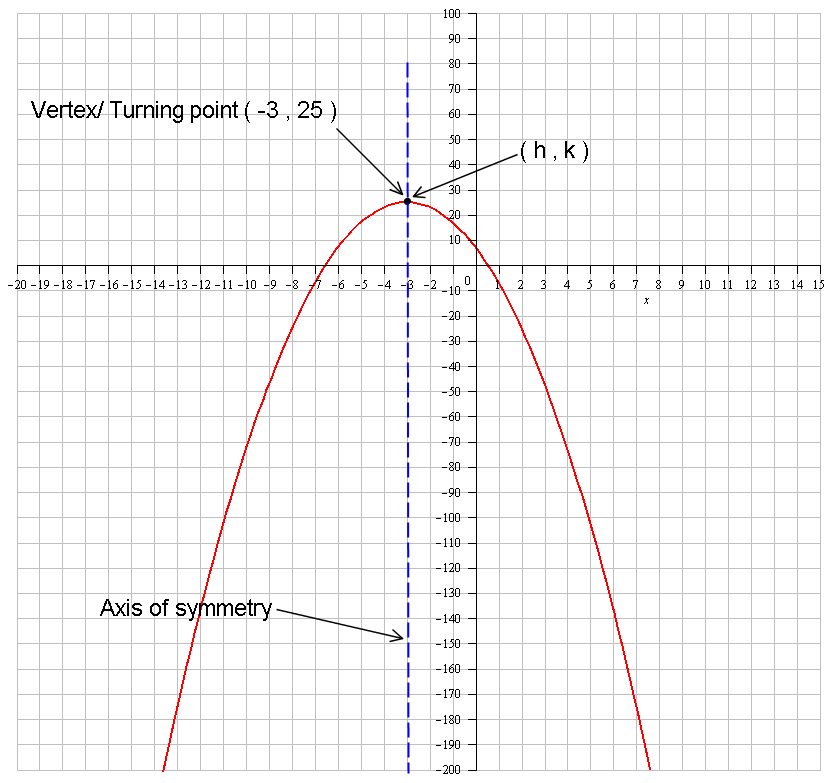
If a equation is like this #-2(x+3)^2+25# what is its turning point?

Question

1237 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-10T08:21:09

#color(blue)((-3 ,25)#

The turning point is the same as the vertex.

If we express a quadratic in the form:

#y=a(x-h)^2+k#

Then:

#bba# is the coefficient of #x^2#, #bbh# is the axis of symmetry and #bbk# is the maximum/minimum value of the function.

Also, if:

#a > 0# then the parabola is of the form #uuu#

if:

#a < 0 # then the parabola is of the form #nnn#

The given function is in this form:

#h = -3#

#k=25#

Since #h# is the axis of symmetry, this is the x coordinate of the vertex, and since #k# is the max/min value it is the y coordinate of the vertex.

So:

#(h,k)->(-3,25)#

This is the vertex and hence the turning point of the function.

This can be seen on the graph:

enter image source here