Here the situation is shown below,
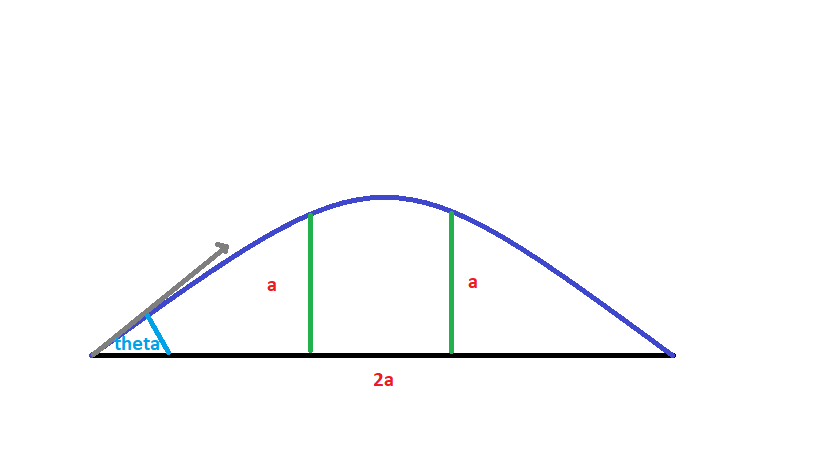
So,let after time tt of its motion,it will reach height aa,so considering vertical motion,
we can say,
a=(u sin theta)t -1/2 g t^2a=(usinθ)t−12gt2 (uu is the projection velocity of projectile)
Solving this we get,
t=(2u sin theta_-^+sqrt(4u^2 sin^2 theta -8ga))/(2g)t=2usinθ+−√4u2sin2θ−8ga2g
So,one value (smaller one) of t=tt=t (let) is suggesting the time to reach aa while going up and the other (larger one) t=t' (let) while coming down.
So,we can say in this time interval the projectilw horizontally travelled distance 2a,
So,we can write, 2a=u cos theta(t'-t)
Putting the values and arranging,we get,
u^4 sin^2 2theta -8gau^2 cos^2 theta-4a^2g^2=0
Solving for u^2,we get,
u^2 =(8gacos^2 theta _-^+sqrt(64g^2a^2 cos^4 theta+16a^2g^2sin^2 2theta))/(2 sin^2 2theta)
Putting back sin 2theta=2 sin theta cos theta we get,
u^2=(8gacos^2 theta _-^+sqrt(64g^2a^2 cos^4 theta+64a^2g^2sin^2 theta cos^2 theta))/(2 sin^2 2theta)
or, u^2=(8ga cos^2 theta+sqrt(64g^2a^2cos^2theta(cos^2 theta+sin^2 theta)))/(2sin^2 2theta)=(8gacos^2theta+8ag cos theta)/(2 sin^2 2theta)=(8agcostheta(cos theta+1))/(2 sin^2 2theta)
now,formula for range of projectile motion is R=(u^2 sin 2 theta)/g
So,multiplying the obtained value of u^2 with (sin2 theta)/g,we get,
R=(2a(cos theta+1))/sin theta=(2a* 2 cos^2(theta/2))/(2 sin (theta/2) cos (theta/2))=2a cot (theta/2)


