Actually, it could, but not often. Occasionally it acts as a Lewis acid to stabilize interactions with a transition metal, for instance.
CYANIDE COMPARES WELL WITH CARBON MONOXIDE
#"CN"^(-)# is isoelectronic with #"CO"#, and it can act as both a #\mathbf(sigma)# donor and #\mathbf(pi)# acceptor.
Its MO diagram looks somewhat like that of #"CO"#:
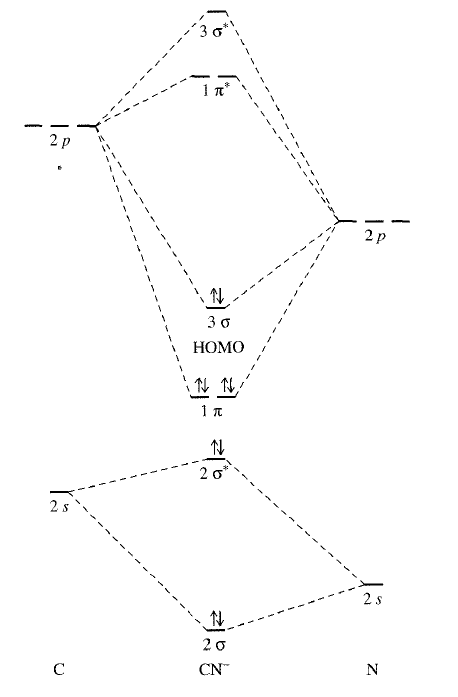
We can see the two electrons in the orbital labeled #3sigma#, which is its HOMO. Also, its two #1pi^"*"# antibonding orbitals are empty, which are its LUMOs.
Thus, it can donate electrons from its #sigma# bonding HOMO and/or accept electrons into its #pi^"*"# antibonding LUMOs. That makes it both a Lewis base and a Lewis acid for the respective reasons.
SOMETIMES, CYANIDE CAN BE A LEWIS ACID
One situation where #"CN"^(-)# acts like a Lewis acid is after it #sigma# bonds via its carbon onto a transition metal to form a metal-ligand complex, such as hexacyanochromate(III), i.e. #["Cr"("CN")_6]^(3-)#.
This behavior can be summarized in the following diagram which is based off of the angular overlap method, which is basically a simplified approach to approximate d-orbital splitting that ignores s and p interactions:
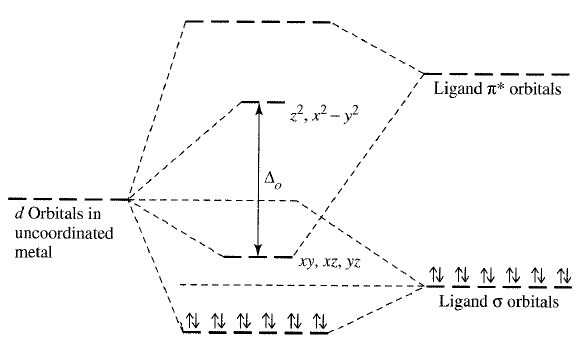
As you can see, it gives a similar d-orbital splitting as one would get from Crystal Field Theory. (However, it gives an inaccurate representation of the ligand #sigma# MO energies!)
At first, #"CN"^(-)# uses its #3sigma# HOMO to interact with the compatible #d_(z^2)# and #d_(x^2-y^2)# atomic orbitals of the transition metal and raises their energy when generating the two #e_g^"*"# orbitals (next to them is the label "#z^2, x^2 - y^2#").
#"CN"^(-)# ends up donating electrons to the metal in a #\mathbf(sigma)# destabilizing interaction. This is Lewis base behavior because it donates electrons.
Then, the #1pi^"*"# antibonding LUMOs of #"CN"^(-)# also happen to be compatible with the #d_(xy)#, #d_(xz)#, and #d_(yz)# atomic orbitals of the transition metal and lowers their energy when generating the three #t_(2g)# orbitals (next to them is the label "#xy,xz,yz#").
This is done by accepting electrons from the metal in what's called a #\mathbf(pi)#-backbonding stabilization. This is Lewis acid behavior because it accepts electrons.
Here is the #pi# backbonding stabilization happening with #"CO"# and a transition metal's #d_(xy)# and #d_(xz)# orbitals.
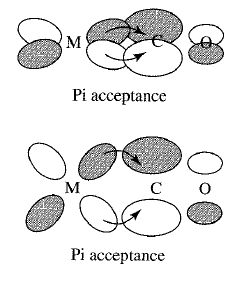
Overall, this increases the ligand field splitting energy, which one might call #Delta_o# for octahedral complexes, because the energy of the three now-lower #t_(2g)# orbitals decreased, and the energy of the two now-higher #e_g^"*"# orbitals increased, relative to the original, uncoordinated #d# atomic orbitals.
Because of the #pi#-acceptor, i.e. Lewis acid behavior of #"CN"^(-)#, it is a very strong field ligand, and it often gives rise to "low spin" complexes where electrons are paired in the #t_(2g)# orbitals first before going into the higher-energy #e_g^"*"# orbitals.

