If #f(x)=(x^2+36)/(2x), 1 <=x<=12#, at what point is f(x) at a minimum?
1 Answer
I would derive your function and do some tests on the derivative to find your points.
Remember that the derivative is a function that tells you about the INCLINATION (slope), at every point, of your original function. This inclination at point
Now, if you can find points where your inclination "changes" (from up to down or vice-versa, represented by ZERO inclination) you find your maxima or minima!!!
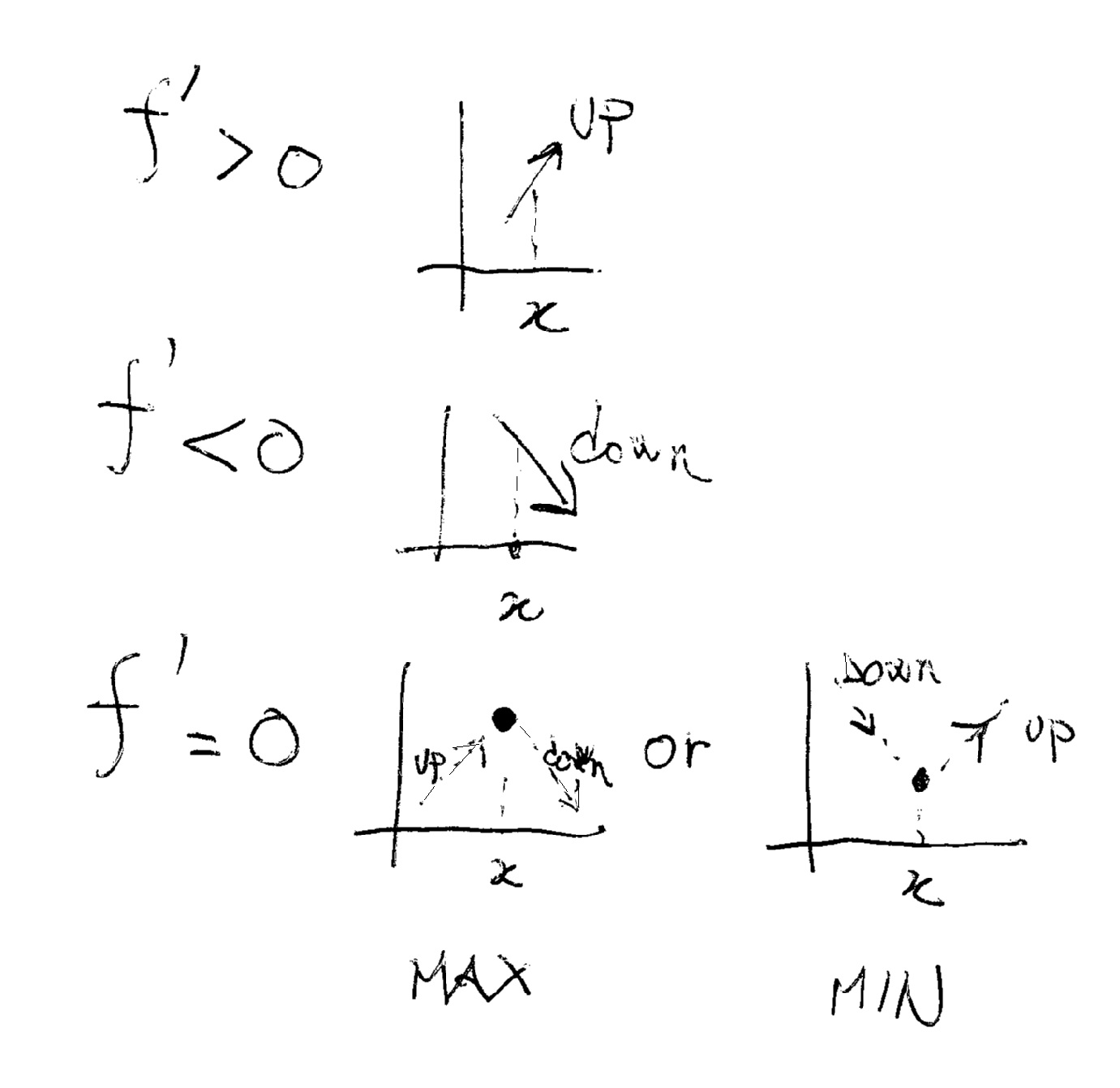
In your case you have:
1) I now sets equal to ZERO to find the point(s)
I get:
Which gives me
This means that when
2) I check when my derivative is bigger than zero, this means that the function goes up and I can "see" whether my points are maxima or minima!
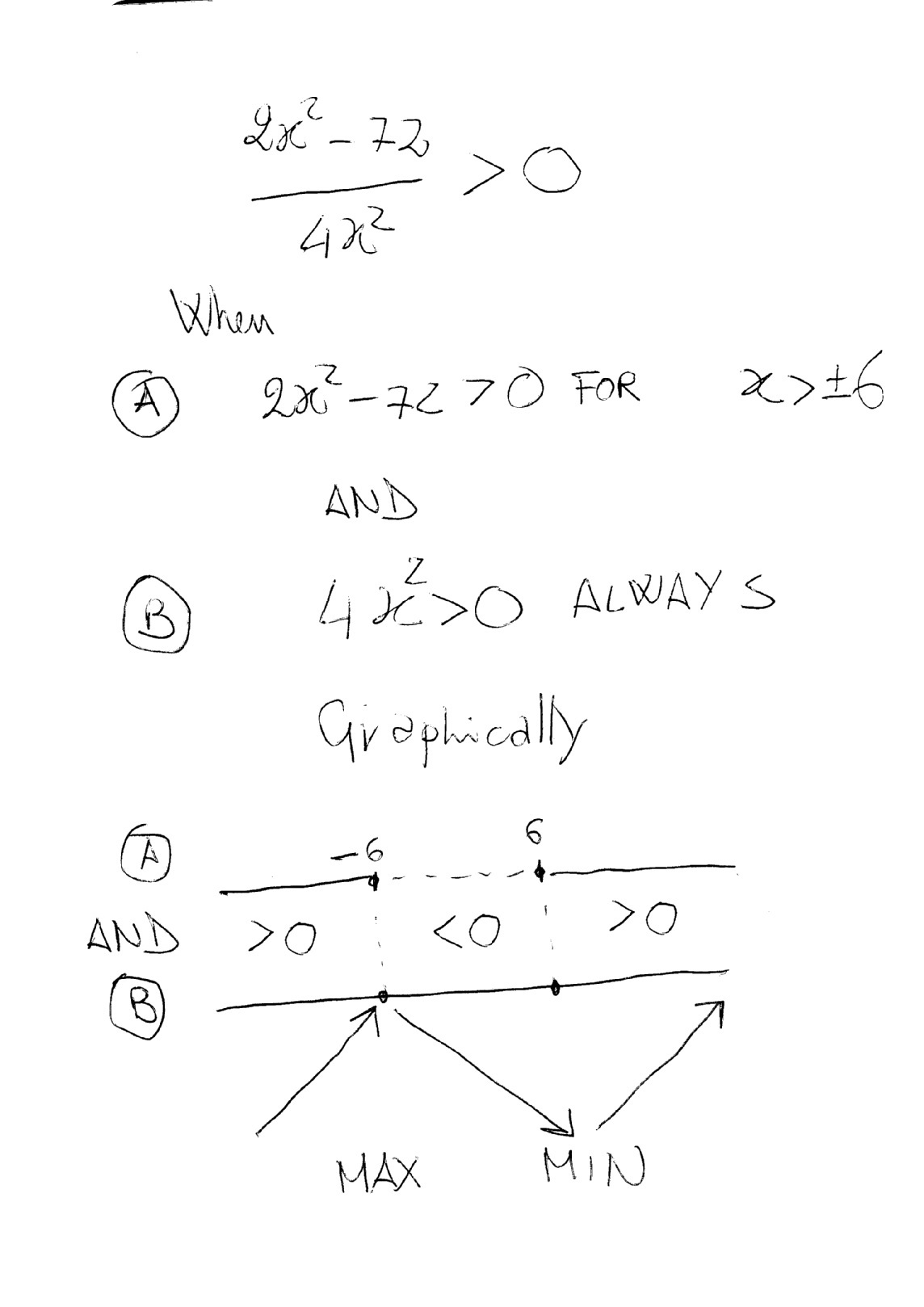
You can see that the point of coordinate
You can also plot your functon to confirm this:
graph{(x^2+36)/(2x) [-14.83, 25.17, -5.37, 14.63]}

