Question

If `f(x)=(x+3)(x-1)^2`, how do you find the local maxima and minima at `x` using the second derivative?

I'm lost. Once I find the derivative of `f(x)`, and then the second derivative using that, what exactly am I supposed to do? Set `f''(x)` equal to `0`, then plug those points into `f'(x)`?

Answer 1

`(1,0)` is a minimum.

`(-5/3, 256/27)` is a maximum.

Explanation:

.

`y=(x+3)(x-1)^2`

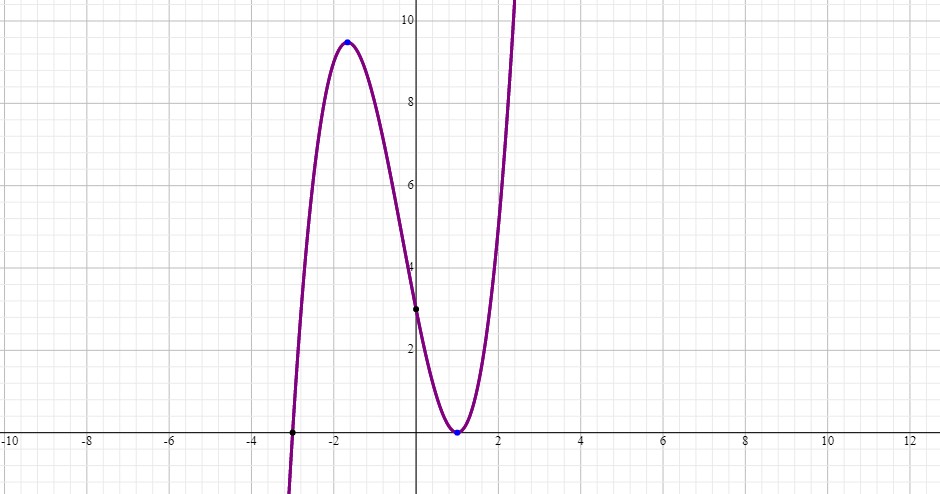
We need to take the first derivative of the function, set it equal to zero, and find its roots. Those roots are where the maxima and minima of the function are (both local and absolute).

`dy/dx=2(x+3)(x-1)+(x-1)^2=0`

`(x-1)(2x+6+x-1)=0`

`(x-1)(3x+5)=0`

`x=1 and -5/3`

Now, we need to perform the first derivative test to find out which one is the minimum and which one the maximum.

We know that the derivative evaluated at any point on the function gives us the slope of the tangent to the curve at that point. As such, is we try values of `x` to the right and left of each of these roots and check whether the derivative is positive or negative at that point, we will figure out the behavior of the function.

Let,s try a value smaller than `1` and another one larger then one:

`x=0, :. dy/dx=-5`

`x=2, :. dy/dx=11`

This means that at `x=0`, the tangent to the curve has a negative slope and at `x=2`, the tangent to the curve has a positive; i.e. the function is decreasing before `x=1` and increasing after it.

As such, `x=1` is the `x`-coordinate of the minimum of the function. we can plug it into the function itself to get its `y`-coordinate:

`x=1, :. y=0, :. (1,0)` is a minimum.

Let's now do the same with `x=-5/3`:

`x=-2, :. dy/dx=3`

`x=-1, :. dy/dx=-4`

At `x=-2`, the slope of the tangent to the curve is positive and at `x=-1`, the slope of the tangent to the curve is negative.

This means `x=-5/3` is the `x`-coordinate of the maximum of the function. Let's plug it into the function itself to find its `y`-coordinate.

`x=-5/3, :. y=256/27, :. (-5/3, 256/27)` is a maximum.

The second derivative is used to find the inflection point. But this problem has not asked for that.

The graph of the function is: