If I don't have a calculator, how can I assess the normality of a data set?
1 Answer
This answer uses a set of actual data representing the results of the last Bucharest English Language Contest for middle school students. We have 313 participants, who have received marks ranging from 65 to 100 on a 0-100 scale . I created a Google sheet where the data set can be analysed, as follows:
- in Sheet 1, we have the raw data set
- in Sheet 2, we have the (ascendingly) ordered data set, plus several descriptive statistics (minimum, maximum, average, mode, quartiles, and standard deviation)
- in Sheet 3, we have a frequency table built for our range of values split into 6 equal intervals, plus the corresponding histogram
Method 1: Visually checking the normality of the data set
Once we have the histogram, we can check the normality of our data set visually (for a step-by-step guide to creating a histogram see this answer using the same data set):
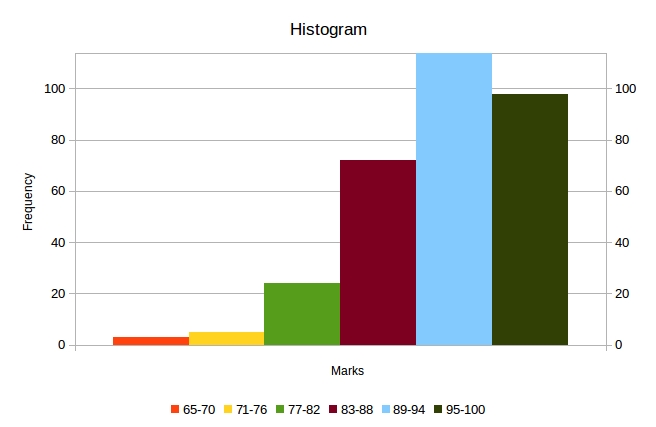
We can see from the histogram that our frequency distribution is not bell shaped , so we can conclude that our data set is not normally distributed . The visual method is quick and intuitive, however it might be unreliable in cases less clear-cut than this one.
Method 2: Assess normality by computing a normality test
Usually, we would choose one of the normality tests (Chi-square, Kolmogorov-Smirnov, Jarque-Bera etc). Each test can be used under specific assumptions. These tests are quite involved mathematically and they cannot be computed easily without a dedicated calculator or software package.
However, there is a calculation that is easier to compute than the above tests, namely the normal counts, that can be used as a quick and intuitive test for normality.
In a normal distribution, the 68-95-99.7 rule applies. This rule says that in a normal distribution:
- 68% of the observations lie within one standard deviation of the mean
- 95% of the observations lie within two standard deviations of the mean
- 99.7% of the observations lie within three standard deviations of the mean.
In order to check for normality, we'll count the number of observations in our data set that lie within 1, 2 and 3 standard deviations from the mean. Afterwards, we compare them to the expected percentage values in a normal distribution (68%-95%-99.7%).
Step 1: calculate the mean
The mean for our data set is 82.5
Step 2: calculate the standard deviation
The standard deviation for our data set is 6.19
Step 3: count the number of observations within 1, 2 and 3 standard deviation(s) from the mean
- the number of observations within
#(MEAN+- 1*STDEV)# is#96 => 30.67%# - the number of observations within
#(MEAN+- 2*STDEV)# is#212 => 67.73%# - the number of observations within
#(MEAN+- 3*STDEV)# is#313 => 100%#
Step 4: compare the observed and expected percentage values
#30.67%# observed vs#68%# expected for#MEAN+- 1*STDEV# #67.73%# observed vs#95%# expected for#MEAN+- 2*STDEV# #100%# observed vs#99.7%# expected for#MEAN+- 3*STDEV#
We can see from the normal counts method that the observed values considerably diverge from the values expected in a normal distribution.

