If O be a inner point of a triangle ABC Then prove that OA+OB+OC < AB+BC+CA ?
1 Answer
Jul 6, 2018
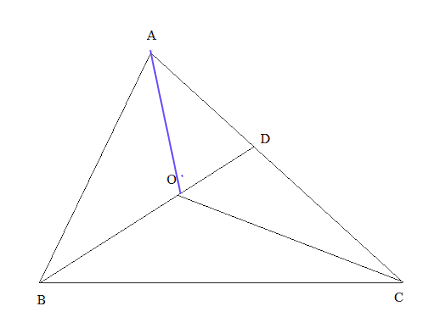
Let O be a inner point of a triangle ABC. We are to prove that
*Construction"
For
For
Adding [1] and [2] we get
Similarly
And
Adding (3),(4)and (5) we get

