Given that
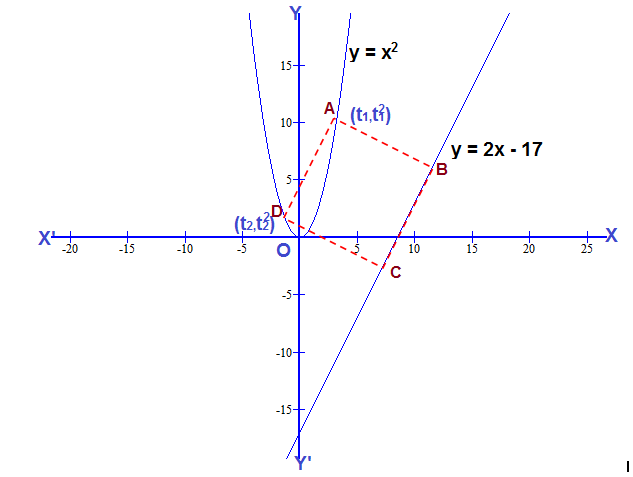
- the equation of parabola #y=x^2#
- the equation of a straight line #y=2x-17#
Let the corner points #A(t_1,t_1^2) and D(t_2,t_2^2) # of the square #ABCD# are on the parabola and other two corner points #BandD# are on the given line #y=2x-17#
So slope of AD #=(t_1^2-t_2^2)/(t_1-t_2)=2-> "the slope of the given line"# , since side AD is parallel to the given line.
Hence we have #t_1+t_2=2#
The length of side #AD=sqrt((t_1-t_2)^2+(t_1^2-t_2^2)^2)#
#=(t_1-t_2)sqrt(1+(t_1+t_2)^2)#
#=(t_1-t_2)sqrt(1+2^2)=sqrt5(t_1-t_2)=2sqrt5(t_1-1)#
Now length of the perpendicular from #A# to the line
#AB=(t_1^2-2t_1+17)/sqrt(1^2+2^2)=(t_1^2-2t_1+17)/sqrt5#
#ABCD# being a square
We have #AB=AD#
#=>(t_1^2-2t_1+17)/sqrt5=2sqrt5(t_1-1)#
#=>t_1^2-2t_1+17-10(t_1-1)=0#
#=>t_1^2-12t_1+27=0#
#=>t_1^2-9t_1-3t_1+27=0#
#=>t_1(t_1-9)-3(t_1-9)=0#
#=>(t_1-9)((t_1-3)=0#
Hence we get
#t_1=3 or 9#
When #t_1= 3#, the area of the square will be minimum
So
#"AREA"_"min"= AD^2# at #t_1=3#
#=(2sqrt5(t_1-1))^2#
#=20xx(3-1)^2#
#=80#squnit


