If sin theta=2/3 with theta in quadrant 1, find sec theta?
2 Answers
Jun 4, 2018
Explanation:
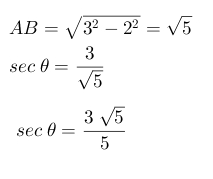
Jun 4, 2018
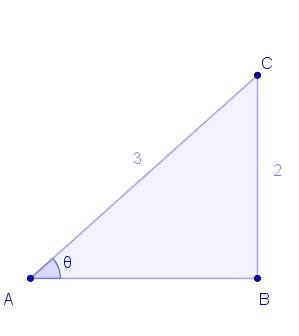
Using right angle trigonometry, we can find out that
Explanation:
To solve this problem, we can use a right triangle. Here is what mine looks like:
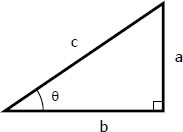
(We know the triangle is in this orientation because theta is in the first quadrant).
We are told that


