If #tan(A/2)=sqrt((1-x)/(1+x))*tan((theta)/2)# then show that #costheta=(cosA-x)/(1-x*cosA)#?
2 Answers
Feb 23, 2018

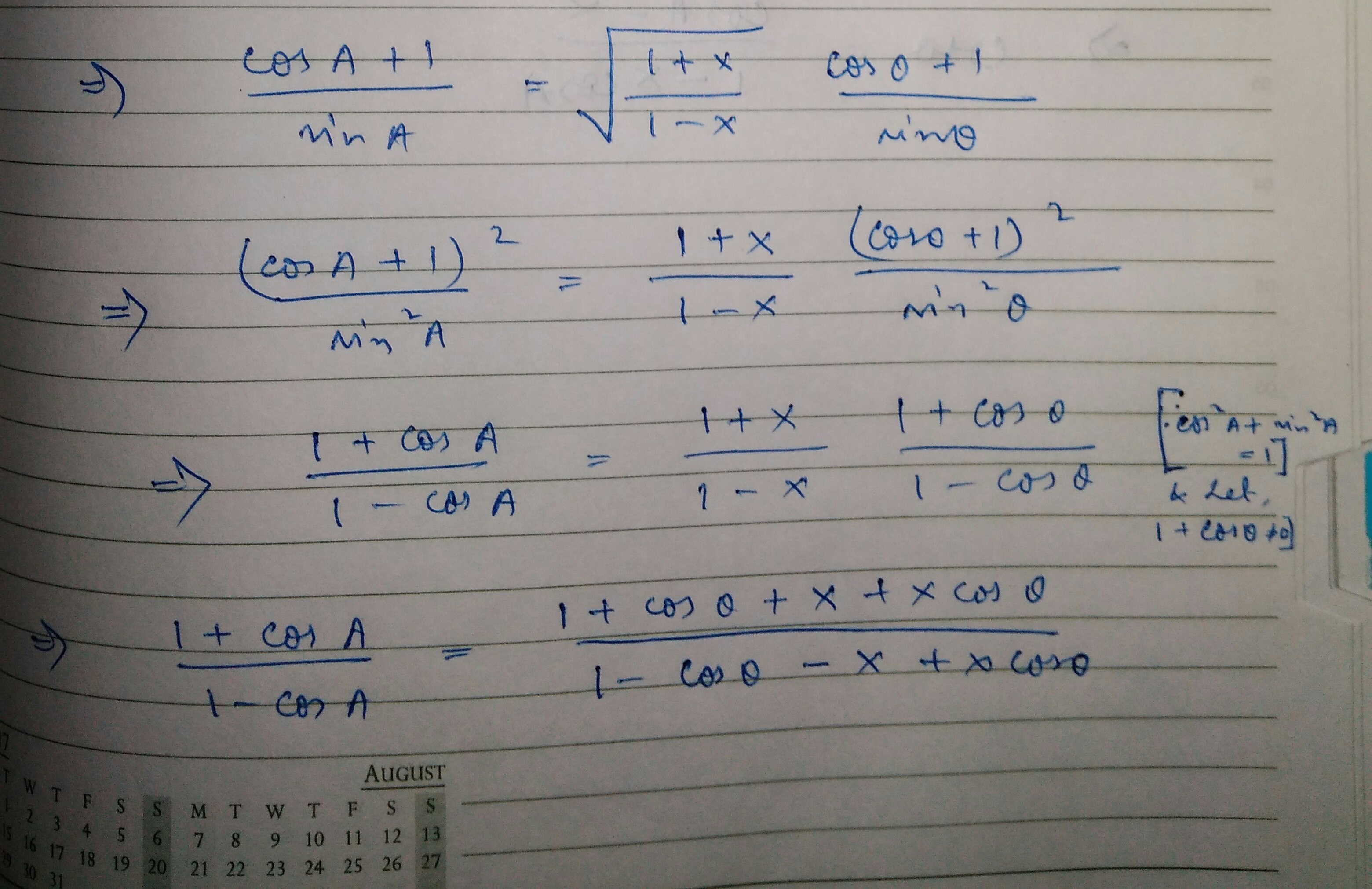
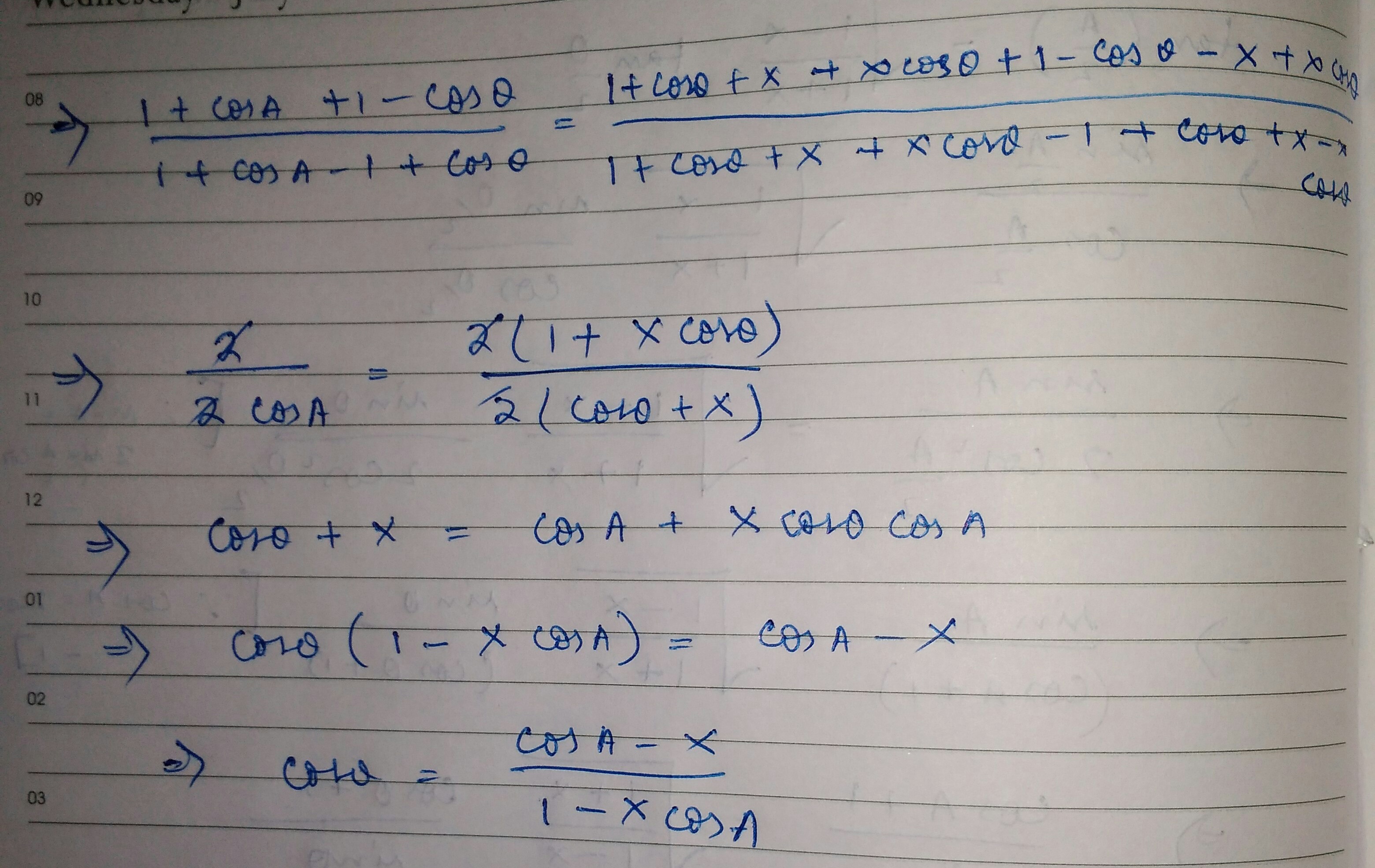
Feb 23, 2018
Given
Now
Inserting the value of


