If the bisector of angle W and angle Y of a cyclic quadrilateral WXYZ meet at A and B respectively then prove that AB is the diameter of the circle. ?
1 Answer
Apr 28, 2018
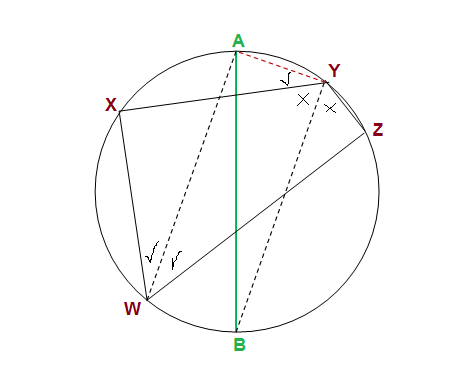
Given
that the bisectors of angle W and angle Y of a cyclic quadrilateral WXYZ meet the circle at A and B respectively.
RTP
To prove that AB is the diameter of the circle.
Construction
Proof
Sum of opposite angles of a cyclic quadrilateral being
Bur
So We have
This means

