If the #["H"_3"O"^(+)]# in a solution is #2*10^-5# #"M"#, what is the #["OH"^(-)]#?
1 Answer
Explanation:
For pure water at room temperature, the concentration of hydronium cations,
#color(blue)(|bar(ul(color(white)(a/a)["H"_3"O"^(+)] * ["OH"^(-)] = 10^(-14)"M"^2color(white)(a/a)|)))#
This relationship is based on the self-ionization of water, which at room temperature produces equal concentrations,
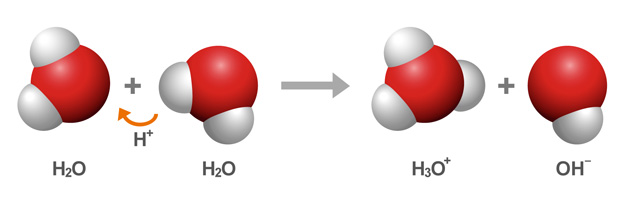
So, you're dealing with an aqueous solution that has
#["H"_3"O"^(+)] = 2 * 10^(-5)"M"#
Right from the start, you can tell that this solution is acidic, since the concentration of hydronium ions increased compared with that of pure water.
Despite the fact that you have more hydronium ions present, the relationship between the hydronium and hydroxide anions remains valid.
This of course implies that the concentration of hydroxide anions will be lower than
More specifically, the concentration of hydroxide anions will be
#["OH"^(-)] = (10^(-14)"M"^color(red)(cancel(color(black)(2))))/(2 * 10^(-5)color(red)(cancel(color(black)("M")))) = color(green)(|bar(ul(color(white)(a/a)5 * 10^(-10)"M"color(white)(a/a)|)))#
As practice, you can find the pH of this solution by using
#color(blue)(|bar(ul(color(white)(a/a)"pH" = - log(["H"_3"O"^(+)])color(white)(a/a)|)))#
In this case, you will have
#"pH" = - log(2 * 10^(-5)) = 4.7#

