Question

If the point (x,#sqrt((3)/2) is on the unit circle, what is x?

(x,#sqrt((3)/2)

Answer 1

`1/2`

Explanation:

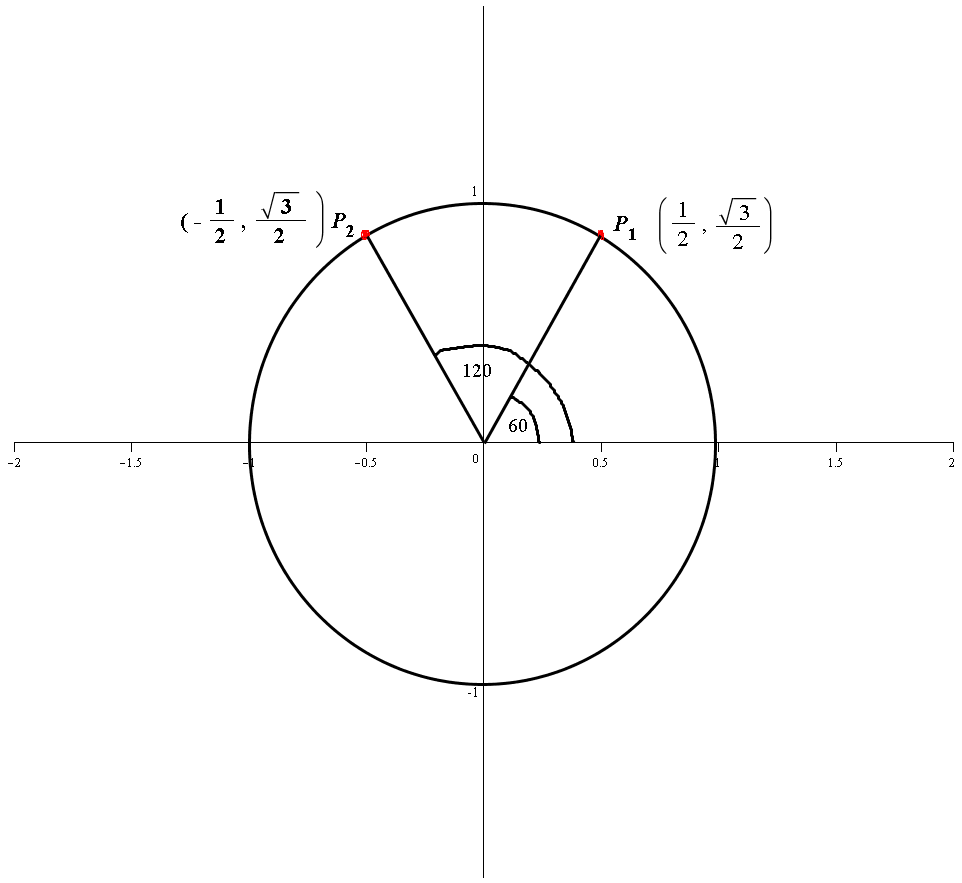
We can represent the point `bbP` on a unit circle having coordinates `( x , y )` as:

`x=rcostheta`

`y=rsintheta`

Since our radius is `1` this simplifies to:

`x=costheta`

`y=sintheta`

So we can say that:

`y=sintheta=sqrt(3)/2`

And:

`theta = arcsin(sqrt(3)/2)=>theta=60^@ , 120^@`

`x=costheta=cos(60)=1/2`

`x=costheta=cos(120)=-1/2`

So our `x` coordinate is `1/2` or `-1/2`

You can see we have two possible positions for `bbP`. This is because a specific angle wasn't given.

This was read as `sqrt(3)/2`, but it maybe it should have been `sqrt(3/2)`. The brackets around the 3, made it unclear. In any case the process is exactly the same.