If the population of the world was 6.5 billion in 2006 and is currently 7.1 billion (in the year 2013), what will the population be in the year 2050?
1 Answer
The answer will depend upon what model of growth you assume will occur.
There is insufficient information to answer this question.
Explanation:
Here are a couple models (neither is likely to be accurate).
In both cases I have used the variable
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Linear Model
The population (in billions) is given by the formula:
We have for the year 2013 i.e.
If this model holds, then for the year 2050 i.e.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Compound Model
The population (in billions) is given by an equation similar to that for the balance of an investment with a compound interest rate,
#color(white)("XXX")p=6.5(1+r)^y
We have for the year 2013 (
If this model holds then for the year 2050 (
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
A more realistic model might look like: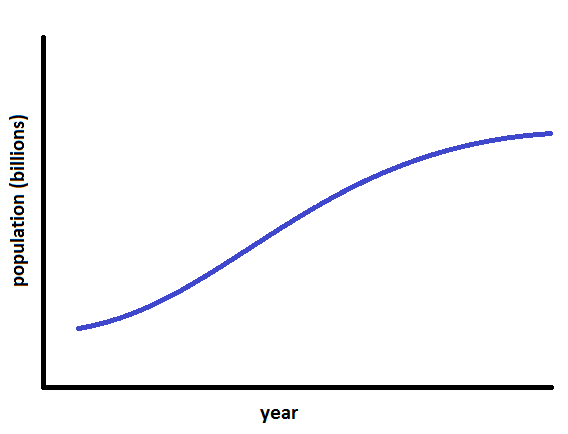
...but the given data provides no information where along this curve the years 2006 and 2013 occur.
