If the relation between #a,b,c# is given as shown below then #a,b,c# are in?
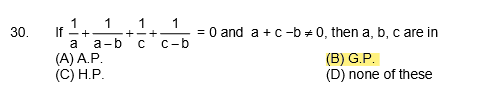
2 Answers
Nov 24, 2017
See below.
Explanation:
From
but
and after dividing both sides by
Nov 24, 2017
Given
As
This means
So


