If the straight lines #ax + by + c = 0# and #x cos(alpha) + y sin(alpha) = c# enclose an angle #pi/4# between them and meet the straight line #x sin(alpha) - y cos(alpha) = 0 # in the same point between them, then?

A) #a^2 + b^2 = c^2#
B) #a^2 + b^2 = 2#
C) #a^2 + b^2 = 2c^2#
D)# a^2 + b^2 = 4#

3 Answers
Cesareo R.
Dec 21, 2017

#a^2+b^2=2#

Explanation:

From the lines

#L_1->ax+by+c=0#
#L_2->x cosalpha+ysinalpha +c=0#

we have

# a cos alpha+b sin alpha = sqrt(a^2+b^2) cos(pi/4)# or

#( a cos alpha+b sin alpha )^2= (a^2+b^2)/2#

but from

#{(x cosalpha+ysinalpha +c=0),(x sin alpha-y cos alpha=0):}#

the intersection point gives us #x=c cos alpha, y = c sin alpha#

and after substituting into

#ax+by+c=0 rArr a cosalpha + b sin alpha = -1#

then

#a^2+b^2=2#

P dilip_k
Dec 22, 2017

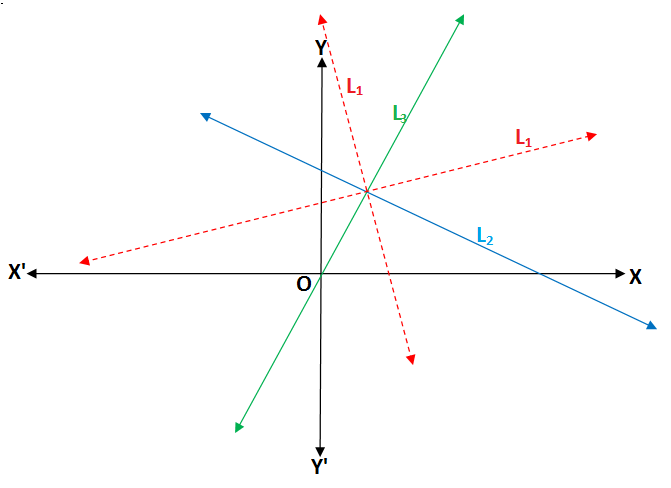
enter image source here
Given lines are

#L_1->ax + by + c = 0#
#L_2->x cos(alpha) + y sin(alpha) = c#
#L_3->x sin(alpha) - y cos(alpha) = 0#

As per given condition above three given lines pass through a fixed point. #L_1# subtends an angle #pi/4# with #L_2# and #L_3# subtends an angle #pi/2# with #L_2# as the product of their slope #=-1#

Hence #L_1# is the bisector of the angle between #L_2 and L_3#. Here two possible orientations of #L_1# have been shown in the figure

Now equations of the angle bisectors between #L_2 and L_3#

#(xsinalpha -ycosalpha)/sqrt(sin^2alpha+cos^2alpha)=pm(xcosalpha+ysinalpha-c)/sqrt(cos^2alpha+sin^2alpha)#
#=>xsinalpha -ycosalpha=pm(xcosalpha+ysinalpha-c)#

Bisector -1
#B_1->#

#x(sinalpha-cosalpha)-y(sinalpha+cosalpha)+c=0#

Bisector 2

#B_2->#

#x(sinalpha+cosalpha)+y(sinalpha-cosalpha)-c=0#

Comparing #L_1 and B_1# we get

#a=sinalpha-cosalpha and b=-(sinalpha+cosalpha)#

So #a^2+b^2=2#

Comparing #L_1 and B_2# we get

#a=-(sinalpha+cosalpha )and b=-(sinalpha-cosalpha)#

So #a^2+b^2=2#

George C.
Dec 22, 2017

B) #a^2+b^2=2#

Explanation:

An alternative quick and dirty method to decide which of the given options is correct is to consider a particular example...

Let #alpha = pi/4# and #c = 3sqrt(2)#

Then the third straight line is:

#xsqrt(2)/2-ysqrt(2)/2 = 0#

which simplifies to #y=x#

The second straight line is:

#xsqrt(2)/2+ysqrt(2)/2 = 3sqrt(2)#

which simplifies to #x+y=6#

These intersect at #(3, 3)#

The first straight line passes through this intersection point and is horizontal or vertical. That is: #y=3# or #x=3#. Expressing these possibilities in the form #ax+by+c=0# we get:

#0x-sqrt(2)y+3sqrt(2) = 0#

or:

#-sqrt(2)x+0y+3sqrt(2) = 0#

In either case #a^2+b^2=2# and matches none of the other options.

Related questions
Impact of this question
17492 views around the world
You can reuse this answer
Creative Commons License