If there is a sphere made up of one hemisphere of Copper and another of iron, On heating what would be its effect and where would its centre of gravity be?
1 Answer
Heating effect : TBC
Centre of gravity : 0.024R from centre on copper side
Explanation:
Determine the location of the centre of gravity.
Define the volume of the sphere as
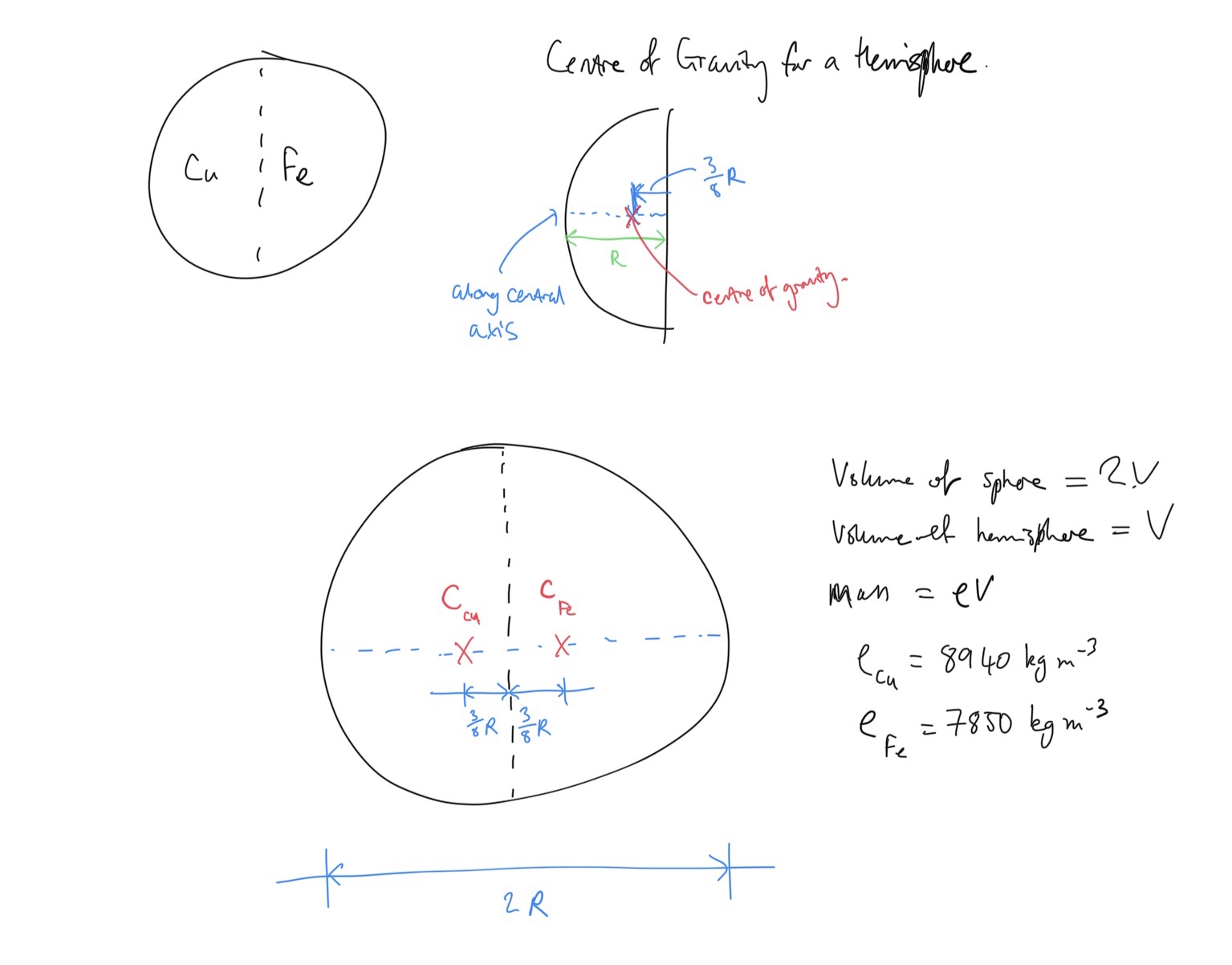
Take moments about the central vertical axis. The resultant moment is equal to the total weight of the sphere multiplied by the perpendicular distance of centre of gravity to the central axis. We know that
Expression for moments about central axis:
Where
Total mass of sphere is sum of masses of hemispheres:
Masses of hemispheres in terms of their densities (remember that the volumes of the hemispheres are equal and we denoted that
Copper:
Iron:
===
The effect upon the sphere during heating.
Copper has a heat capacity of 385 J kg⁻¹ K⁻¹
Iron has a heat capacity of 449 J kg⁻¹ K⁻¹
If the sphere was heated we could assume that the two hemispheres were heated equally; equal transfer of energy to each hemisphere. In that case the temperature of copper would increase further than that of iron (the specific heat capacity tells us that copper requires less energy to increase its temperature by the same amount).
However the above assumes that the masses of the hemispheres are equal, but they are not. As we saw in the solution for the centre of mass copper has a larger density. So the mass of the copper hemisphere is larger than that of the iron one by a factor of 1.14. Its specific heat capacity is smaller by a factor of 1.17. So the overall effect is going to be that the copper half increases its temperature only very slightly more than the iron half.
Equations to illustrate the above conclusion:
So now we can write:
Substitute the ratios from above into that equation:
That tells us that the temperature rise of the iron half will be 97% of the temperature rise of the copper half.
The temperature difference between the hemispheres would lead to a thermal imbalance. This means that there will be a net heat energy transfer from the copper half to the iron half until they reach thermal equilibrium (when heat transfer between the hemispheres is equal).

