If #\vec{g}# is in standard position with terminal point (5, 5) and #\vec{h}# is in standard position with terminal point (4, 2), how do you find the direction of the resultant vector?
1 Answer
So, resultant vector =
The vector is from (0,0) to (9,7) (Direction can also be determined from Triangle Law of addition of vectors)
To find the direction, slide the
The vectors will be something like below after sliding
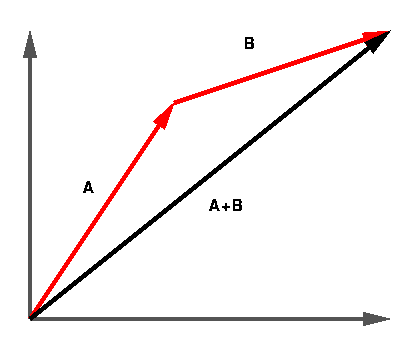
Image Source : http://www.lnk2lrn.com/ap_physicssummer.html


