If we draw a potential energy (U) vs distance (r) curve for a mass 'm' in the gravitational field of the Earth 'M' then why the graph does not exist for r=0 to r=R (where R is the radius of the Earth)but starts from r=R to r=infinity?
1 Answer
Gravitational potential function inside Earth.
The gravitational field strength due to uniform solid sphere within it can be shown to decrease linearly with
Figure below shows the gravitational field strength for both regions inside and outside the sphere.
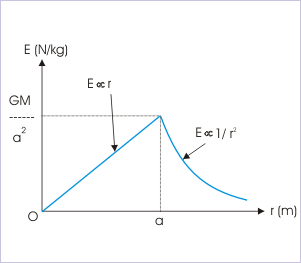
As such Gravitational field function for values of distance
Substituting value of density
Using steps similar to used in above derivation, Gravitational potential function for values of
#U(r)=-G(m_rm)/r#
#=>U(r)=-G(Mmr^2)/a^3# .......(1)
where#m_r# is mass of smaller sphere of radius#r# .
Gravitational potential function outside Earth.
We know that Gravitational potential energy function outside the spherical body is given by the expression
which has a value on the surface of planet
We know that gravitational potential of a point is defined as work done on a unit mass in moving it to that point from
Therefore, total Gravitational potential of a body of mass
We also note that even though Gravitational potential function exists there is no physical significance attributed to Potential inside the Earth calculated with the help of equation (1) as it is physically not possible to take unit mass inside the solid earth, perform actual measurements and compare results. This remains theoretical exercise.
Therefore, from practical point graph is not drawn for values of distances lower than radius of planet as shown below.
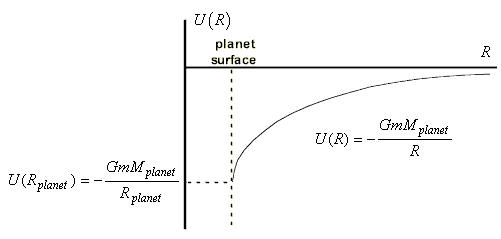
For the purpose of calculations of escape velocity from earth and calculations regarding satellite orbits etc, potential at the surface of earth only is required.
