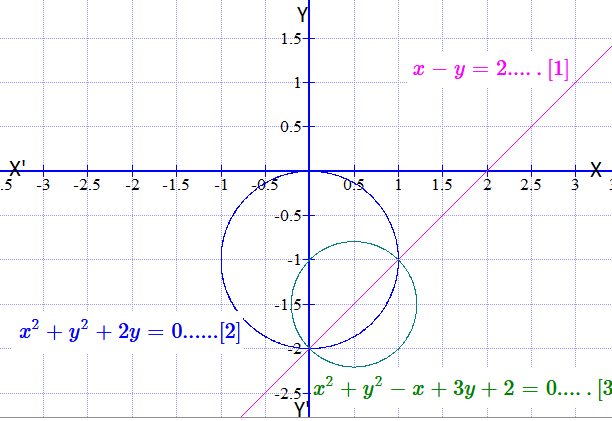
If #x-y=2# is the equation of a chord of the circle #x^2+y^2+2y=0#.Find the equation of the circle of which this chord is a diameter.?
2 Answers
Given that
-
the equation of the chord
#" "color (magenta)(x-y=2.....[1])# -
the equation of the circle
#" "color(blue)(x^2+y^2+2y=0......[2])#
From these two equations we get
So
Inserting in [1] we get
So the coordinates of points intersections of the chord with the circles are
The line segment of the chord is also the diameter of a circle.
So equation of this circle having diameter
This is the required equation of the circle
Explanation:
We will solve this Problem using the following Result R :
R : The Equation (eqn.) of a Circle that passes through
the Points (pt.) of Intersection of a Circle S & Line L
where,
Let,
Note that, the Reqd. Circle, say
Applying R, we may suppose that,
This shows that the Centre
Now, given that
Therefore,
already derived by Respected dk_ch Sir!
Enjoy Maths.!

