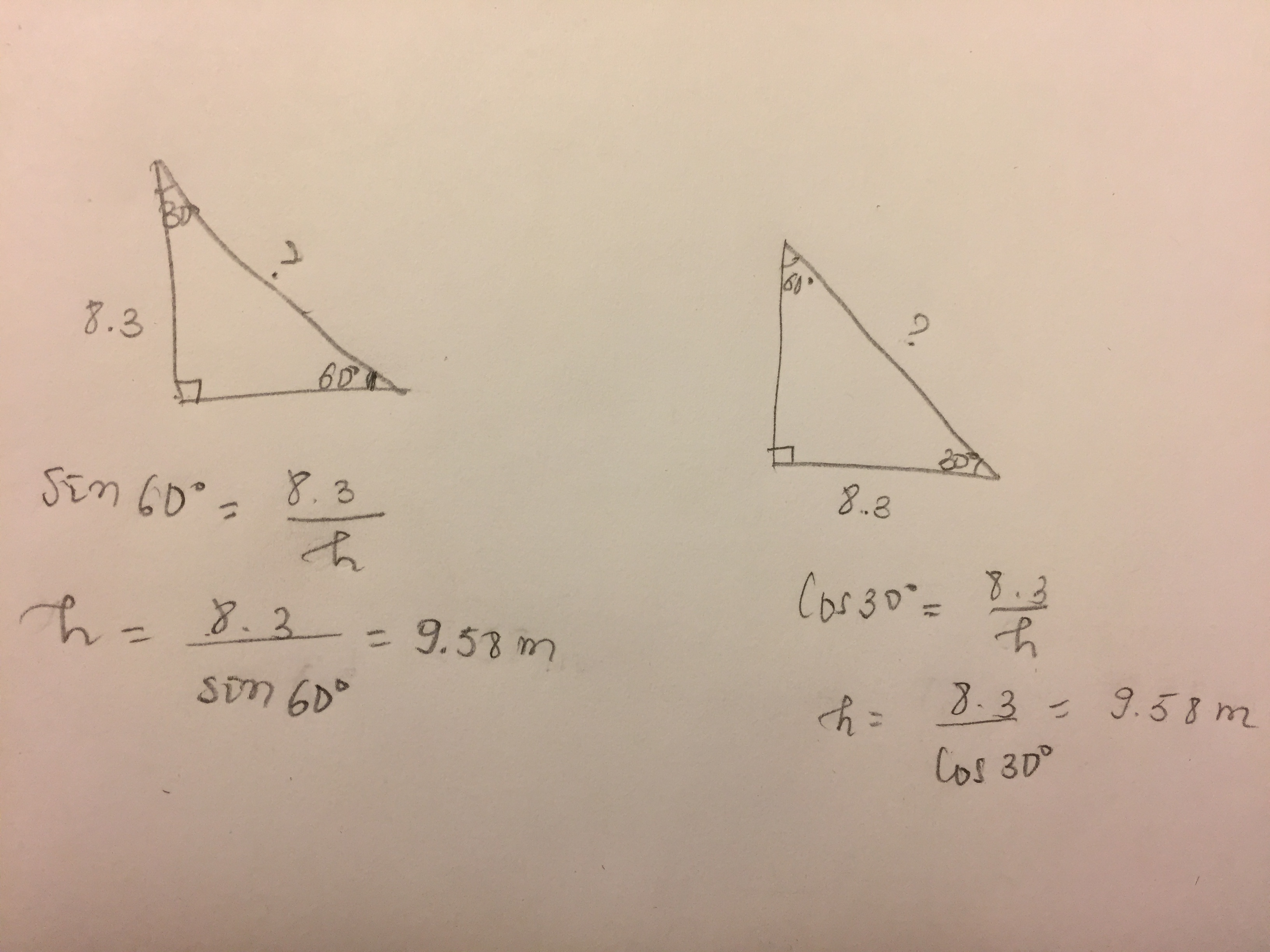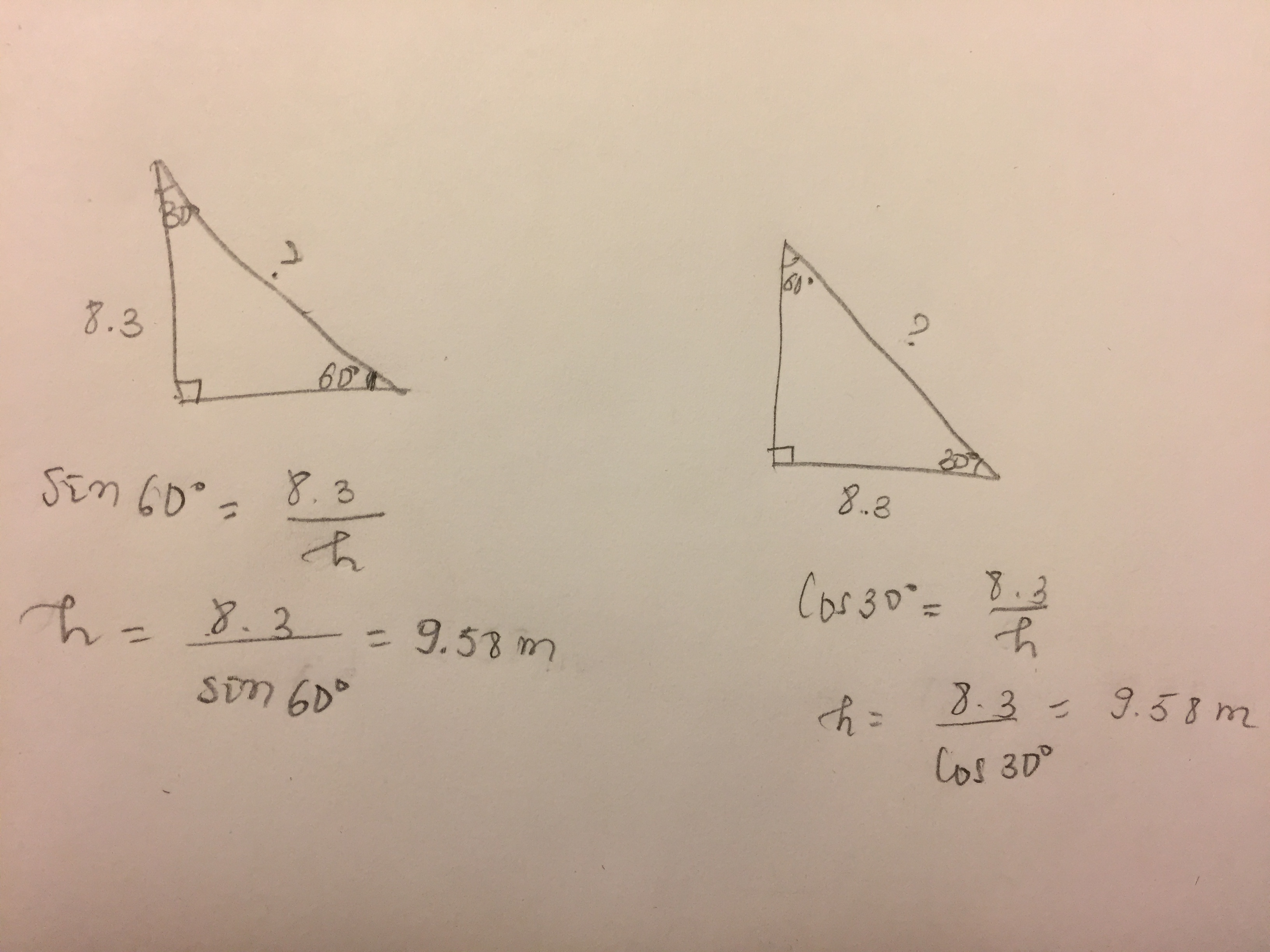Wherever you choose to put your 60˚ angle, you have to remember that the length of its opposite side is 8.3m.
I chose my 60˚ angle as being the angle opposite to the right angle, which means the remaining angle is 30˚.
We know, sin theta=y/h (y being the opposite side of angle theta and h being the Hypotenuse)
theta = 60˚, y=8.3m and h is the unknown.
sin theta=y/h=>sin60˚=8.3/h=>h=8.3/(sin60˚)=9.58m
Another way to do this is to choose the 30˚ angle as the angle opposite to your right angle. Here you will use cos30˚ instead of sin60˚ because they said 8.3m is the length of the side opposite the 60˚ angle and that means your 8.3m is now x (the adjacent of 30˚).
cos theta=x/h=>cos30˚=8.3/h=>h=8.3/(cos30˚)=9.58m
Note that cosine of 30˚ is the same as the sine of 60˚. Realizing that is going to help you memorize the unit circle easily.
If you did not understand, please take a look at the picture.
Hope this helps :)