Question

In a game of pool, the cue ball strikes another ball of the same mass and initially at rest. After the collision, the cue ball moves at 1.10 m/s along a line making an angle of 29.0° with its original direction of motion, and the second ball has a speed ?

Answer 1

Velocity of 2nd ball after collision`~~0.61m/s` and
velocity of cue ball before collision `~~1.26m/s`

Explanation:

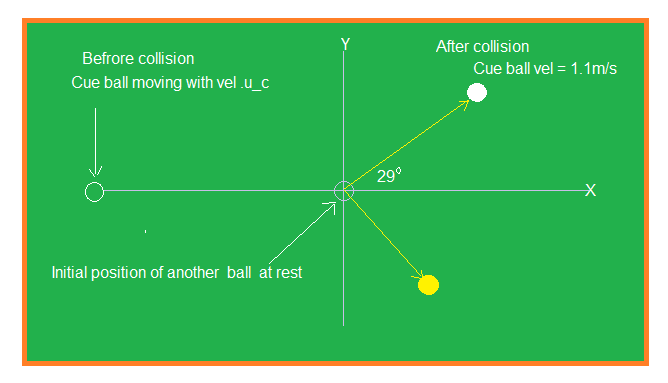
Let
Before collision he Cue ball is moving along the positive direction of X-axis and another ball is at rest lying at origin as shown in adjoining figure.

• `m->"the mass of each ball"`
• `u_c->"Velocity of cue ball before collision"`
• `u_a->"Initial velocity of another ball hit by cue ball"`
• `v_c->"Velocity of cue ball after collision"`
• `v_a->"velocity of another ball after collision"`
• `alpha="Angle subtended by" v_c "with its initial direction of motion"`
• `beta="Angle subtended by"v_a"with the initial direction of motion of cue ball.."`

Given

`v_c=1.1ms^-1 " ";u_a=0;" "alpha = 29^@`

We are to find out the value of `v_a`

To solve this problem let us assume that the collision is perfectly elastic and both conservation of KE and Conservation of linear momentum are valid here.

Applying law conservation of KE we can write

`1/2xxmxxu_c^2+1/2mxxu_a^2=1/2xxmxxv_c^2+1/2xxmxxv_a^2`

`=>u_c^2+u_a^2=v_c^2+v_a^2`

Inserting `u_a=0` we get `" "u_c^2=v_c^2+v_a^2.....(1)`

Now applying law of conservation of momentum

Along X-axis we can write

`mxxu_c+ mxxu_a=mxxv_cxxcosalpha+mxxv_axxcosbeta`

Inserting `u_a=0` we have

`u_c=v_cxxcosalpha+v_axxcosbeta.....(2)`

Now applying law of conservation of momentum

along Y-axis we can write. ( there was no component of initial ovelocity along Y-axis)

`0=mxxv_cxxsinalpha-mxxv_axxsinbeta`

`0=v_cxxsinalpha-v_axxsinbeta.....(3)`

Now squaring eqation (2) and (3) and adding we get

`u_c^2=v_c^2(cos^2alpha+sin^2alpha)+v_a^2(cos^2beta+sin^2beta)+2v_cv_a(cosalphacosbeta-sinalphasinbeta)`

`=>u_c^2=v_c^2+v_a^2+2v_cv_a(cosalphacosbeta-sinalphasinbeta)`

Now combining equation(1) with this we get

`2v_cv_a(cosalphacosbeta-sinalphasinbeta)=0`

`=>cos(alpha+beta)=0`

`=>alpha+beta=90`

putting given value`" "alpha=29^@` we get

`29^@+beta=90=>beta=61^@`

Now inserting the value of `alpha,beta,v_c` in equation(3)

we can write

`1.1*sin29^@-v_a*sin61^@=0`

`:.v_a=(1.1*sin29^@)/(sin61^@)~~0.61m/s`

The velocity of cue ball before collision

`u_c=sqrt(v_c^2+v_a^2)=sqrt(1.1^2+0.61^2)~~1.26m/s`