In a trapezium ABCD , side BC is parallel to AD.Also the lengths of side AB,BC,CD and AD are 8,2,8 and 10 units respectively.Find the radius of the circle that passes through all four points A,B,C and D?
1 Answer
Explanation:
The following is a figure for the question. So the whole thing looks like this one http://below.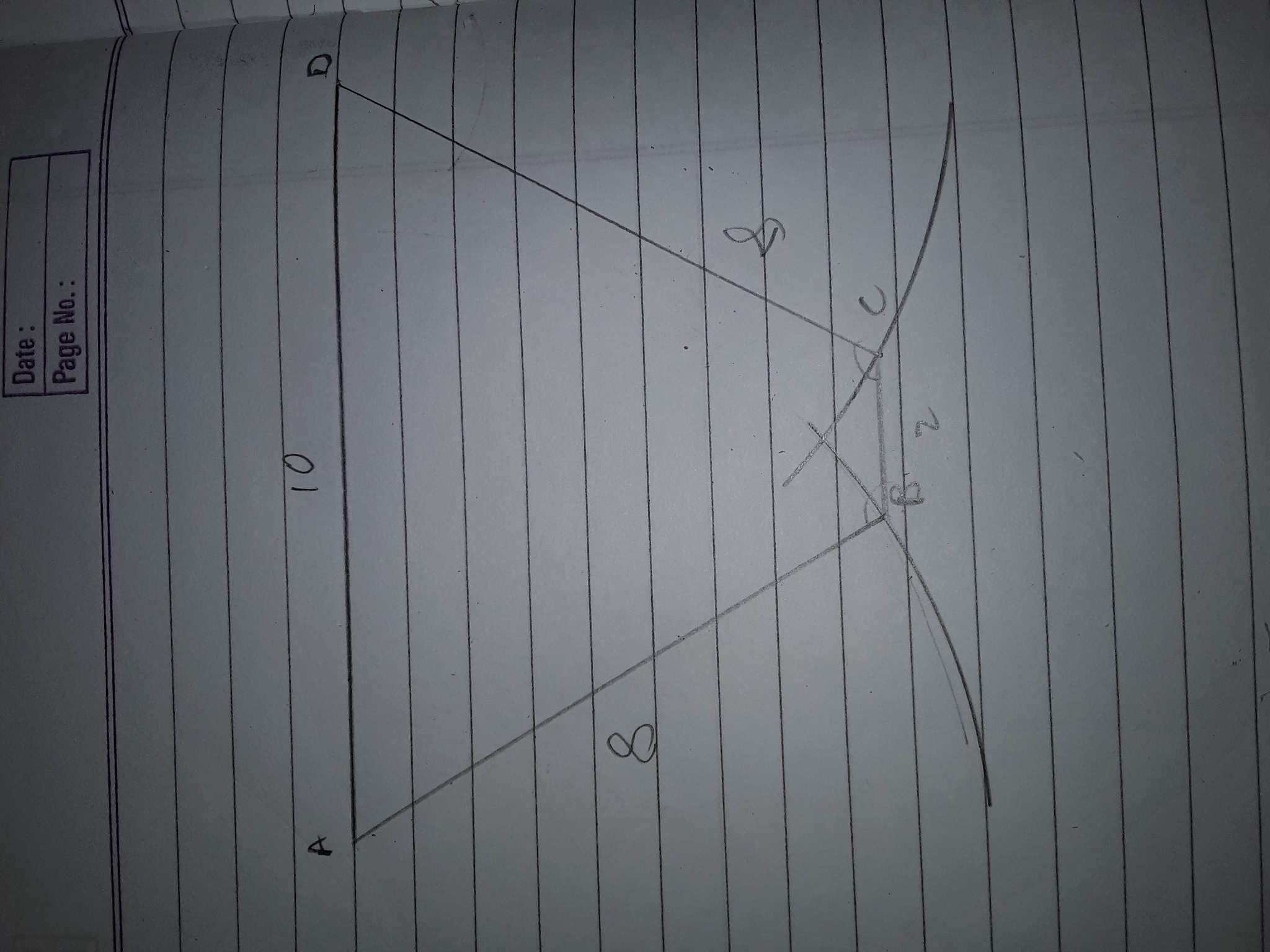
Lets make some construction
Rest things are mentioned in figure.
Now applying pythagorean theorem
We get
Before proceeding any further i would like to tell that i'll find circumcentre of
Since it is a isoceles trapezium
Now , here's a relation
Using cosine rule
Now again using that relation
Hope that helps.


