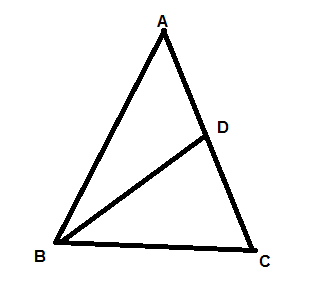
Given
#"In "DeltaABC#
#AB=AC and D" is a point on"AC " such that"#
#BCxxBC=ACxxAD#
#"We are to prove "BD=BC#
Proof
Rearrenging the given relation
#BCxxBC=ACxxAD" "# We can write
#(BC)/(CD)=(AC)/(BC)->DeltaABC" similar "DeltaBDC#
Their corresponding angle pairs are:
#1. /_BAC "= corresponding "/_DBC#
#2. /_ABC "= corresponding "/_BDC#
#3. /_ACB " =corresponding "/_DCB#
So as per above relation 2 we have
#/_ABC =" corresponding "/_BDC#
#"Again in"DeltaABC#
#AB=AC->/_ABC=/_ACB=/_DCB#
#:."In "DeltaBDC,/_BDC=/_BCD#
#->BD=BC#
Alternative way
The ratio of corresponding sides may be written in extended way as follows
#(BC)/(CD)=(AC)/(BC)=(AB)/(BD)#
From this relation we have
#(AC)/(BC)=(AB)/(BD)#
#=>(AC)/(BC)=(AC)/(BD)->"As "AB=AC" given"#
#=>1/(BC)=1/(BD)#
#=>BC=BD#
Proved
Hope, this will help


