In a triangle ABC angle B=60 angle C=45 AND D divides BC internally in the ratio 1:3.?

Question

#THEN (sin BAD)/(sin CAD) IS?#

11738 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-22T15:20:52

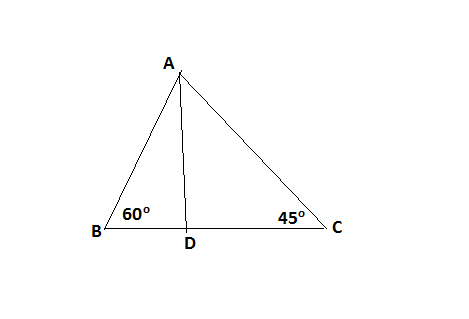
drawn

In the above figure

In #Delta ABC#, #/_ABC=60^@,/_ACB=45^@#

#(BD)/(DC)=1/3......[1]#

Now applying sine rule for #Delta ABD# we can write

#(sin/_BAD)/(sin/_ADB)=(BD)/(AB)......[2]#

And applying sine rule for #Delta ADC# we can write

#(sin/_CAD)/(sin/_ADC)=(DC)/(AC)#

#=>(sin/_CAD)/(sin(180-/_ADB))=(DC)/(AC)#

#=>(sin/_CAD)/(sin/_ADB)=(DC)/(AC).....[3]#

Dividing [2] by [3] we get

#(sin/_BAD)/(sin/_CAD)=(BD)/(DC)xx(AC)/(AB).....[4]#

Now applying sine rule for #Delta ABC# we can write

#(AC)/(AB)=(sin60^@)/(sin45^@)......[5]#

Combining [1], [4] and [5]

#(sin/_BAD)/(sin/_CAD)=1/3xx(sin60^@)/(sin45^@)#

#=>(sin/_BAD)/(sin/_CAD)=1/3xxsqrt3/2xxsqrt2/1=1/sqrt6#