In how many ways can you rearrange the letters A, B, C, D, E?
2 Answers
Jul 20, 2018
Explanation:
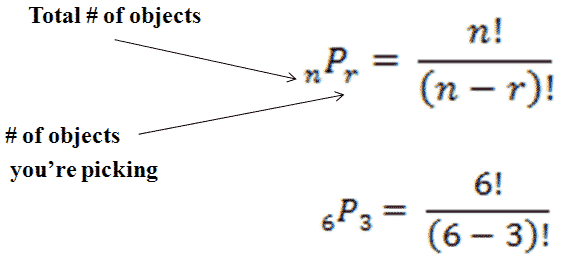
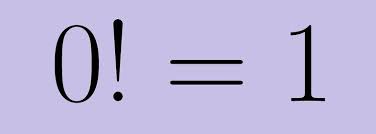

Jul 22, 2018
Explanation:
The total number of linear arrangements obtained from


